-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Bài 7 trang 28 SGK Hình học 12
Cho hình chóp S.ABCD. Gọi A', B', C', D' theo thứ tự là trung điểm của SA, SB, SC, SD. Tỉ số thể tích của hai khối chóp S.A'B'C'D' và S.ABCD bằng:
Đề bài
Cho hình chóp \(S.ABCD\). Gọi \(A', B', C', D'\) theo thứ tự là trung điểm của \(SA, SB, SC, SD\). Tỉ số thể tích của hai khối chóp \(S.A'B'C'D'\) và \(S.ABCD\) bằng:
(A) \(\displaystyle {1 \over 2}\) (B) \(\displaystyle{1 \over 4}\)
(C) \(\displaystyle{1 \over 8}\) (D) \(\displaystyle{1 \over {16}}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng kết quả sau:
Cho khối chóp \(S.ABC\), trên các cạnh \(SA, SB, SC\) lấy các điểm \(A', B', C'\). Khi đó ta có: \[\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}\]
Lưu ý công thức trên chỉ được phép dùng đối với chóp tam giác, khi không là chóp tam giác phải sử dụng phân chia và lắp ghép các khối đa diện trước khi sử dụng công thức.
Lời giải chi tiết
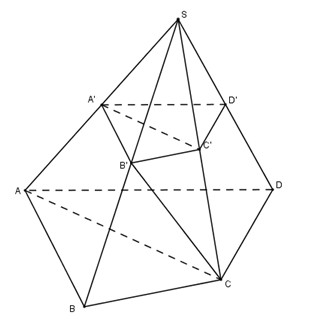
Ta có: \({V_{S.A'B'C'D'}} = {V_{S.A'B'C'}} + {V_{S.A'C'D'}}\)
\({\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}= {\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{8}}}\)
\({ \Rightarrow {V_{S.A'B'C'}} = \dfrac{1}{8}.{V_{S.ABC}} ={ \dfrac{1}{8}.\dfrac{1}{2}.{V_{S.ABCD}} = \dfrac{1}{{16}}{V_{S.ABCD}}}}\)
\({\dfrac{{{V_{S.A'C'D'}}}}{{{V_{S.ACD}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SC'}}{{SC}}.\dfrac{{SD'}}{{SD}} = {\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{8}}}\)
\({ \Rightarrow {V_{S.A'C'D'}} = \dfrac{1}{8}{V_{S.ACD}} = {\dfrac{1}{8}.\dfrac{1}{2}{V_{S.ABCD}} = \dfrac{1}{{16}}{V_{S.ABCD}}}}\)
\( \Rightarrow {V_{S.A'B'C'D'}} = {V_{S.A'B'C'}} + {V_{S.A'C'D'}} \) \(= \dfrac{1}{{16}}.{V_{S.ABCD}} + \dfrac{1}{{16}}.{V_{S.ABCD}} = {\dfrac{1}{8}.{V_{S.ABCD}}}\)
Chọn (C).
Chú ý và sai lầm: KHÔNG ĐƯỢC sử dụng công thức trên như sau: \(\dfrac{{{V_{S.A'B'C'D'}}}}{{{V_{S.ABCD}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}\dfrac{{SC'}}{{SC}}.\dfrac{{SD'}}{{SD}} \) \(= \dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{{16}}\), đây là công thức SAI.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 8 trang 28 SGK Hình học 12
- Bài 9 trang 28 SGK Hình học 12
- Bài 10 trang 28 SGK Hình học 12
- Bài 6 trang 28 SGK Hình học 12
- Bài 5 trang 28 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
