-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Bài 10 trang 27 SGK Hình học 12
Cho hình lăng trụ đứng tam giác ABC.A'B'C'
Video hướng dẫn giải
Cho hình lăng trụ đứng tam giác \(ABC.A'B'C'\) có tất cả các cạnh đều bằng \(a\).
LG a
a) Tính thể tích khối tứ diện \(A'BB'C\).
Phương pháp giải:
Gọi \(M\) là trung điểm của \(B'C'\). Chứng minh \(A'M \bot \left( {BCC'B'} \right)\). Áp dụng công thức \({V_{A'BB'C}} = \dfrac{1}{3}A'M.{S_{BB'C}}\).
Lời giải chi tiết:
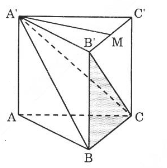
a) Ta tính thể tích hình chóp \(\displaystyle A'.BCB'\).
Gọi \(\displaystyle M\) là trung điểm của \(\displaystyle B'C'\), ta có: \(\displaystyle A'M \bot B'C'\) (1)
Lăng trụ \(\displaystyle ABC.A'B'C'\) là lăng trụ đứng nên:
\(\displaystyle BB' \bot (A'B'C') \Rightarrow BB' \bot A'M\) (2)
Từ (1) và (2) suy ra \(\displaystyle A'M \bot (BB'C')\) hay \(\displaystyle A'M\) là đường cao của hình chóp \(\displaystyle A'.BCB'\).
Ta có: \(\displaystyle A'M\) = \(\displaystyle {{a\sqrt 3 } \over 2};{S_{BB'C}} = {1 \over 2}{a^2}\)
\(\displaystyle \Rightarrow {V_{A'BB'C}} = {1 \over 3}.A'M.{S_{BB'C}}\) \( \Rightarrow {V_{A'BB'C}} =\displaystyle {{{a^3}\sqrt 3 } \over {12}}\)
Cách khác:
Ta chia khối lẳng trụ đã cho thành hình chóp \(A’.ABC, C.A’B’C’\) và \(C.A’BB’\)
Ta có: \({V_{A'.ABC}} = {V_{A'B'C'}} =\displaystyle \frac{1}{3}Sh\) trong đó \(S\) là diện tích đáy \(S = {\rm{ }}{S_{ABC\;}} = {\rm{ }}{S_{ABC}}\) và \(h\) là chiều cao của hình lăng trụ
Lại có: \({V_{ABC.ABC}}\; = {\rm{ }}S.h\)
Do đó, \({V_{C.A'B'B}} =\displaystyle Sh - \frac{1}{3}Sh - \frac{1}{3}Sh = \frac{1}{3}Sh\)
Trong đó, tam giác \(ABC\) là tam giác đều có độ dài cạnh bằng \(a\) nên \(\displaystyle {S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\)
Vì đây là hình lăng trụ đứng nên \(h = AA’ = BB’= CC’ = a.\)
Vậy thể tích hình chóp \(C.A’BB’\) là:
\({V_{C.A'B'B}} = \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{{12}}\)
LG b
b) Mặt phẳng đi qua \(A'B'\) và trọng tâm tam giác \(ABC\), cắt \(AC\) và \(BC\) lần lượt tại \(E\) và \(F\). Tính thể tích hình chóp \(C.A'B'FE\).
Phương pháp giải:
Phân chia và lắp ghép các khối đa diện: \(V = {V_{B'.CEF}} + {V_{B'.A'EC}} = {V_1} + {V_2}\)
Lời giải chi tiết:
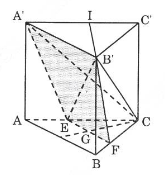
Thể tích hình chóp \(\displaystyle C.A'B'EF\) bằng tổng thể tích hai hình chóp:
- \(\displaystyle V_1\) là thể tích hình chóp đỉnh \(\displaystyle B'\), đáy là tam giác \(\displaystyle CEF\).
- \(\displaystyle V_2\) là thể tích hình chóp đỉnh \(\displaystyle B'\), đáy là tam giác \(\displaystyle A'EC\).
Do \(\displaystyle (ABC) // (A'B'C')\) nên dễ thấy \(\displaystyle EF // AB\). Ta cũng có: \(\displaystyle EF\) = \(\displaystyle {2 \over 3}a\)
Hình chóp \(\displaystyle B'.CEF\) có chiều cao \(\displaystyle BB' = a\) và diện tích đáy là: \(\displaystyle {S_{C{\rm{EF}}}}=\frac{1}{2}EF.CG = {1 \over 2}.{{2a} \over 3}.{2 \over 3}.{{a\sqrt 3 } \over 2} = {{{a^2}\sqrt 3 } \over 9}\)
Từ đây ta có: \(\displaystyle {V_1} = {{{a^3}\sqrt 3 } \over {27}}\)
Do \(\displaystyle EC = {2 \over 3}AC\) nên \(\displaystyle {S_{A'BE}} = \frac{1}{2}A'A.EC = \frac{1}{2}.a.\frac{2}{3}a = \frac{{{a^2}}}{3}\)
Gọi \(\displaystyle I\) là trung điểm của \(\displaystyle A'C'\) ta có: \(\displaystyle \left\{ \begin{array}{l}B'I \bot A'C\\B'I \bot AA'\end{array} \right. \Rightarrow B'I \bot \left( {ACC'A'} \right) \Rightarrow B'I \bot \left( {A'EC} \right)\)
Hình chóp \(\displaystyle B'.A'EC\) có chiều cao là \(\displaystyle B'I\) bằng \(\displaystyle {{a\sqrt 3 } \over 2}\) nên \(\displaystyle {V_2} = \frac{1}{3}.B'I.{S_{A'EC}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{{{a^2}}}{3} = \frac{{{a^3}\sqrt 3 }}{{18}}\)
Vậy thể tích hình chóp \(\displaystyle C.A'B'FE\) là: \(\displaystyle V = V_1 + V_2\) = \(\displaystyle {{5{a^3}\sqrt 3 } \over {54}}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 11 trang 27 SGK Hình học 12
- Bài 12 trang 27 SGK Hình học 12
- Bài 1 trang 27 SGK Hình học 12
- Bài 2 trang 27 SGK Hình học 12
- Bài 3 trang 27 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
