Phần câu hỏi bài 1 trang 86 Vở bài tập toán 9 tập 2

Câu 1

Hãy điền những từ thích hợp vào chỗ trống (......) trong các câu sau :

a) Hai cung được gọi là bằng nhau nếu ...........................................

b) Trong hai cung, cung nào có số đo .......... được gọi .....................

Phương pháp giải:

Ta sử dụng kiến thức về so sánh hai cung :

Trong một đường tròn hay hai đường tròn bằng nhau:

- Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.

- Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Lời giải chi tiết:

a) Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.

b) Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Câu 2.

Cho đường tròn tâm \(O\), đường kính \(AB.\) Lấy điểm \(C\) trên đường tròn sao cho \(\widehat {BOC} = 30^\circ .\) Số đo của cung nhỏ \(AC\) tính bằng độ là :

\(\left( A \right)\,\,90^\circ ;\,\,\,\,\,\,\left( B \right)\,\,100^\circ ;\)

\(\left( C \right)\,\,120^\circ ;\,\,\,\,\,\,\left( D \right)\,\,150^\circ .\) 

Khoanh tròn vào chữ cái trước kết quả đúng.

Phương pháp giải:

+ Số đo của nửa đường tròn bằng \(180^\circ .\)

+ Nếu \(C\) là một điểm nằm trên cung \(AB\)  thì số đo cung \(AB = \)số đo cung \(AC + \) số đo cung \(BC\).

Lời giải chi tiết:

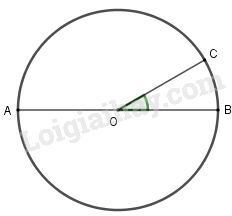
Vì C thuộc cung \(AB\) nên số đo sung \(BC + \) số đo cung \(AC = \) số đo cung \(AB.\)

Mà \(AB\) là đường kính nên số đo cung \(AB = 180^\circ \) và \(\widehat {BOC} = 30^\circ \) nên số đo cung \(BC = 30^\circ .\)

Suy ra \(30^\circ  + \) số đo cung \(AC\)\( = 180^\circ \) nên số đo cung \(AC\) bằng \(180^\circ  - 30^\circ  = 150^\circ. \) Vậy số đo cung nhỏ \(AC\) là \(150^\circ .\)

Chọn D.

Câu 3.

Cho đường tròn \(\left( O \right)\) đi qua ba đỉnh của một tam giác nhọn. Các cung nhỏ \(AB,BC,CA\) có số đo lần lượt là \(x - 20^\circ ,x + 10^\circ ,x + 40^\circ .\) Khi đó, số đo của góc \(AOB\) bằng :

\(\left( A \right)\,\,75^\circ ;\,\,\,\,\,\,\,\left( B \right)\,\,85^\circ\),

\(\left( C \right)\,\,90^\circ ;\,\,\,\,\,\,\,\,\left( D \right)\,\,95^\circ .\)

Khoanh tròn vào chữ cái trước kết quả đúng. 

Phương pháp giải:

Sử dụng: Cả đường tròn có số đo \({360^0}.\)

Số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó.

Lời giải chi tiết:

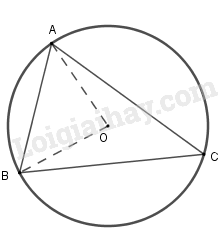
Vì cả đường tròn có số đo bằng \(360^\circ \) nên

Số đo cung \(AB + \) số đo cung \(AC + \) số đo cung \(BC = 360^\circ \)

Hay \(x - 20^\circ  + x + 40^\circ  + x + 10^\circ  = 360^\circ  \\\Leftrightarrow 3x = 330^\circ  \Leftrightarrow x = 110^\circ \)

Suy ra số đo cung \(AB\) là \(110^\circ  - 20^\circ  = 90^\circ .\)

Suy ra \(\widehat {AOB} = 90^\circ \) (góc ở tâm chắn cung  nhỏ \(AB\)).

Chọn C.

Loigiaihay.com