Phần câu hỏi bài 9 trang 116 Vở bài tập toán 9 tập 2

Giải phần câu hỏi bài 9 trang 116 VBT toán 9 tập 2. Một lục giác đều nội tiếp đường tròn bán kính R. Tỉ số độ dài của cạnh lục giác đều với độ dài của cung bị căng là...

Lựa chọn câu để xem lời giải nhanh hơn

Câu 21

Một lục giác đều nội tiếp đường tròn bán kính R.

Tỉ số độ dài của cạnh lục giác đều với độ dài của cung bị căng là:

(A) 1 : 6 (B) \(1\,\,:\,\,\pi \)

Khoanh tròn vào chữ cái trước kết quả đúng.

Phương pháp giải:

+ Xác định độ dài cạnh của lục giác đều

+ Tính độ dài cung bị căng theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\) với \(n^\circ \) là số đo cung bị căng.

Lời giải chi tiết:

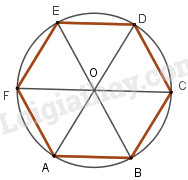
Vì các cạnh của lục giác đều bằng nhau nên ta có 6 cung bằng nhau và số đo mỗi cung bằng \(\dfrac{{360^\circ }}{6} = 60^\circ .\)

Khi đó, độ dài cung nhỏ \(AB\) là \({l_{AB}} = \dfrac{{\pi R.60}}{{180}} = \dfrac{{\pi R}}{3}\)

Lại có \(\widehat {AOB} = 60^\circ \) (=sđ\(\overparen{AB}\))

mà tam giác \(OAB\) cân tại \(O\) (do \(OA = OB\)) suy ra \(OAB\) là tam giác đều

Từ đó \(AB = OA = R.\)

Tỉ số cần tìm là \(AB:{l_{AB}} = R:\dfrac{{\pi R}}{3} = 3:\pi \).

Chọn C.

Câu 22

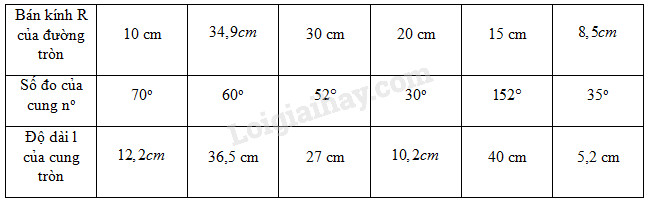
Lấy giá trị gần đúng của \(\pi \) bằng 3,14. Hãy điền vào ô trống (…) trong bảng sau (làm tròn đến chữ số thập phân thứ nhất và đến độ):

Phương pháp giải:

Sử dụng công thức tính độ dài cung \(l = \dfrac{{\pi Rn}}{{180}}\) với \(n^\circ \) là số đo cung và \(R\) là bán kính đường tròn.

Từ đó suy ra \(n = \dfrac{{180l}}{{\pi R}};\,R = \dfrac{{180l}}{{\pi n}}\) .

Lời giải chi tiết:

+ \(R = 10cm;n = 70 \Rightarrow l = \dfrac{{\pi Rn}}{{180}}\)\( = \dfrac{{3,14.10.70}}{{180}} \approx 12,2cm\)

+ \(n = 60;\,l = 36,5 \Rightarrow R = \dfrac{{180l}}{{\pi n}}\)\( = \dfrac{{180.36,5}}{{3,14.60}} \approx 34,9cm\)

+ \(R = 30cm;l = 27cm \Rightarrow n = \dfrac{{180l}}{{\pi R}}\)\( = \dfrac{{180.27}}{{3,14.30}} \approx 52\)

+ \(R = 20cm;n = 30 \Rightarrow l = \dfrac{{\pi Rn}}{{180}}\)\( = \dfrac{{3,14.20.30}}{{180}} \approx 10,5cm\)

+ \(R = 15cm;l = 40cm \Rightarrow n = \dfrac{{180l}}{{\pi R}}\)\( = \dfrac{{180.40}}{{3,14.15}} \approx 152\)

+ \(n = 35;l = 5,2cm \Rightarrow R = \dfrac{{180l}}{{\pi n}}\)\( = \dfrac{{180.5,2}}{{3,14.35}} \approx 8,5cm\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 7 phiếu

Bài tiếp theo

Bài 41 trang 116 Vở bài tập toán 9 tập 2
Giải bài 41 trang 116 VBT toán 9 tập 2. Lấy giá trị gần đúng của pi bằng 3,14. Hãy điền vào ô trống (…) trong bảng sau (đơn vị độ dài: cm, làm tròn đến chữ số thập phân thứ nhất và đến độ)...
Bài 42 trang 117 Vở bài tập toán 9 tập 2
Giải bài 42 trang 117 VBT toán 9 tập 2. a) Tính độ dài cung 60 độ của một đường tròn có bán kính 3 dm.b) Tính chu vi vành xe đạp có đường kính 650 mm...
Bài 43 trang 117 Vở bài tập toán 9 tập 2
Giải bài 43 trang 117 VBT toán 9 tập 2. Cho ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Chứng minh rằng độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC...
Bài 44 trang 117 Vở bài tập toán 9 tập 2
Giải bài 44 trang 117 VBT toán 9 tập 2. Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh xe có đường kính là 1,672 m và bánh xe trước có đường kính là 88 cm...
Bài 45 trang 118 Vở bài tập toán 9 tập 2
Giải bài 45 trang 118 VBT toán 9 tập 2. Bánh xe của một ròng rọc có chu vi 540 mm. Dây cu roa bao bánh xe theo cung AB có độ dài 200 mm. Tính góc AOB (h.56)...
Bài 46 trang 118 Vở bài tập toán 9 tập 2
Giải bài 46 trang 118 VBT toán 9 tập 2. Vĩ độ của Hà Nội là 20 độ 01 phút. Mỗi vòng kinh tuyến Trái Đất khoảng 40000 km. Tính độ dài cung kinh tuyến từ Hà Nội đến xích đạo...
Bài 47 trang 119 Vở bài tập toán 9 tập 2
Giải bài 47 trang 119 VBT toán 9 tập 2. Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O’, đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O’) tại B...