Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây

Phần câu hỏi bài 3 trang 116 Vở bài tập toán 9 tập 1

Giải phần câu hỏi bài 3 trang 116 VBT toán 9 tập 1. Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC, CA...

Lựa chọn câu để xem lời giải nhanh hơn

Câu 5

Hãy khoanh trong vào chữ cái đứng trước đáp án đúng.

Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC, CA và O là giao điểm của các đường trung trực của tam giác đó. Biết rằng OD > OE > OF. Khi đó ta có:

(A) AB > BC > AC

(B) BD > AC > AB

(D) BC < AC <AB

Phương pháp giải:

Vận dụng kiến thức : Dây nào lớn hơn thì dây đó gần tâm hơn.

Lời giải chi tiết:

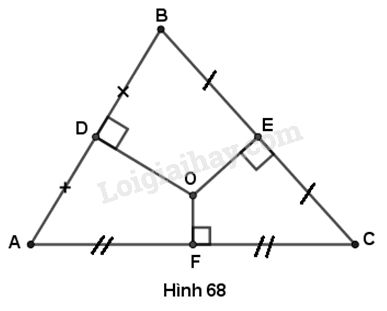
Vì \(OD > OE > OF \Rightarrow AB < BC < AC.\)

Chọn C.

Câu 6

Cho đường tròn (O) đường kính 10cm, dây AB cách tâm O một khoảng 3cm. Độ dài dây AB bằng:

(A) 4cm (B) 6cm

Phương pháp giải:

- Vẽ hình theo giả thiết đã cho.

- Gọi khoảng cách từ tâm \(O\) đến dây \(AB\) là \(OH.\)

- Áp dụng định lí Py-ta-go và định lí đường kính vuông góc với một dây thì đi qua trung điểm của dây đó để tìm \(AB.\)

Lời giải chi tiết:

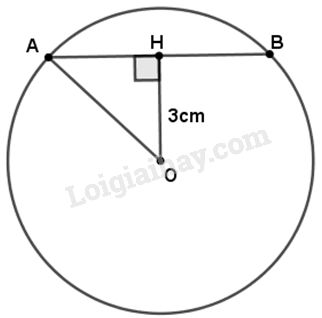
Đường tròn \(\left( O \right)\) có đường kính là \(10cm\) nên \(AO = R = 10:2 = 5\left( {cm} \right).\)

Từ \(O\) kẻ đường thẳng vuông góc với dây \(AB\), cắt dây \(AB\) tại \(H.\)

Khi đó, \(OH\) là khoảng cách từ tâm \(O\) đến dây \(AB.\)

Tam giác vuông \(AHO,\) theo định lí Py-ta-go ta có : \(AH = \sqrt {A{O^2} - O{H^2}} \)\( = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right).\)

Đường kính của đường tròn tâm \(O\) chứa \(OH\) vuông góc với \(AB\) nên \(AH = HB = 4\left( {cm} \right).\) (định lí trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó)

Vậy \(AB = AH + HB \)\(= 4 + 4 = 8\left( {cm} \right).\)

Chọn C.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 5 phiếu

Bài tiếp theo

Bài 9 trang 117 Vở bài tập toán 9 tập 1
Giải bài 9 trang 117 VBT toán 9 tập 1. Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm...
Bài 10 trang 117 Vở bài tập toán 9 tập 1
Giải bài 10 trang 117 VBT toán 9 tập 1. Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E ...
Bài 11 trang 118 Vở bài tập toán 9 tập 1
Giải bài 11 trang 118 VBT toán 9 tập 1. Cho đường tron (O). Gọi AC, AD là hai dây bằng nhau của đường tròn...
Bài 12 trang 118 Vở bài tập toán 9 tập 1
Giải bài 12 trang 118 VBT toán 9 tập 1. Cho hình 72 trong đó hai đường tròn có cùng tâm O. Cho biết AB > CD...
Bài 13 trang 119 Vở bài tập toán 9 tập 1
Giải bài 13 trang 119 VBT toán 9 tập 1. Cho đường tròn tâm (O), điểm A nằm bên ngoài vòng tròn. Vẽ dây BC vuông góc với OA tại A...