Bài 5. Ứng dụng thực tế các tỉ số lượng giác của góc nh..

Bài 37 trang 103 Vở bài tập toán 9 tập 1

Giải bài 37 trang 103 VBT toán 9 tập 1. Một người trinh sát đứng cách một tòa nhà khoảng 10m. Góc nâng từ chỗ anh ta đứng đến nóc nhà là 40^o ...

Đề bài

Một người trinh sát đứng cách một tòa nhà khoảng 10m. Góc nâng từ chỗ anh ta đứng đến nóc nhà là 40^o

a) Tính chiều cao của tòa nhà

b) Nếu anh ta định chuyển sao cho góc nâng là 35^o thì anh ta cách tòa nhà bao nhiêu mét? Khi đó anh ta tiến lại gần hay ra xa tòa nhà ? (làm tròn đến chữ số thập phân thứ hai).

Phương pháp giải - Xem chi tiết

a) Tính chiều cao của nóc nhà bằng cách vận dụng kiến thức cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối.

b) Thay đổi giá trị của góc \(B\) và giải tương tự câu a.

Lời giải chi tiết

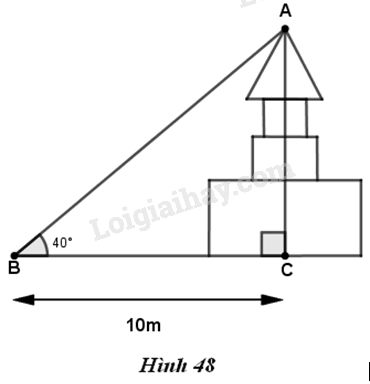
Trong hình \(48,\) ta coi \(BC\) là khoảng cách từ người trinh sát đến tòa nhà ; \(AC\) là chiều cao của tòa nhà.

a) Trong tam giác vuông \(ABC,\) ta có :

\(AC = BC.\tan \widehat {ABC} = 10.\tan {40^o} \)\(\approx 8,39\left( m \right)\)

Vậy tòa nhà cao khoảng \(8,39\left( m \right).\)

b) Khi \(\widehat B = {35^o}\) thì :

\(BC = \dfrac{{AC}}{{\tan \widehat {ABC}}}\)\( = \dfrac{{8,39}}{{\tan {{35}^o}}} \approx 11,982\left( m \right),\) tức là người trinh sát đứng cách tòa nhà khoảng \(12m.\)

Như vậy, anh ta tiến xa ngôi nhà hơn.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài tiếp theo

Bài 38 trang 103 Vở bài tập toán 9 tập 1
Giải bài 38 trang 103 VBT toán 9 tập 1. Thang AB dài 5,5m tựa vào tường làm thành một góc 62o so với mặt đất (h.49)...
Bài 39 trang 103 Vở bài tập toán 9 tập 1
Giải bài 39 trang 103 VBT toán 9 tập 1. Đài quan sát ở Toronto, Ontario (Canada) cao 533m...
Bài 40 trang 104 Vở bài tập toán 9 tập 1
Giải bài 40 trang 104 VBT toán 9 tập 1. Một máy bay ở độ cao 10km. Khi bay hạ cánh xuống mặt đất...
Bài 41 trang 105 Vở bài tập toán 9 tập 1
Giải bài 41 trang 105 VBT toán 9 tập 1. Một người quan sát ở đài hải đăng cao 800 feet (đơn vị đo lường Anh)...
Bài 36 trang 102 Vở bài tập toán 9 tập 1
Giải bài 36 trang 102 VBT toán 9 tập 1. Từ đỉnh một tòa nhà cao 60m, người ta nhìn thấy một ô tô đang đỗ cạnh một góc 28^o ...