-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Giải SBT toán hình học và giải tích 12 cơ bản
Câu hỏi trắc nghiệm chương 2: Mặt nón, mặt trụ, mặt cầu
Bài 2.46 trang 66 SBT hình học 12
Giải bài 2.46 trang 66 sách bài tập hình học 12. Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy,...
Đề bài
Cho hình nón tròn xoay có đỉnh là \(S\), \(O\) là tâm của đường tròn đáy, đường sinh bằng \(a\sqrt 2 \) và góc giữa đường sinh và mặt phẳng đáy bằng \({60^0}\). Diện tích xung quanh \({S_{xq}}\) của hình nón và thể tích \(V\) của khối nón tương ứng là:
A. \({S_{xq}} = \pi {a^2},V = \dfrac{{\pi {a^3}\sqrt 6 }}{4}\)
B. \({S_{xq}} = \dfrac{{\pi {a^2}}}{2},V = \dfrac{{\pi {a^3}\sqrt 3 }}{{12}}\)
C. \({S_{xq}} = \pi {a^2}\sqrt 2 ,V = \dfrac{{\pi {a^3}\sqrt 6 }}{4}\)
D. \({S_{xq}} = \pi {a^2},V = \dfrac{{\pi {a^3}\sqrt 6 }}{{12}}\)
Phương pháp giải - Xem chi tiết
- Diện tích xung quanh \({S_{xq}} = \pi rl\).
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
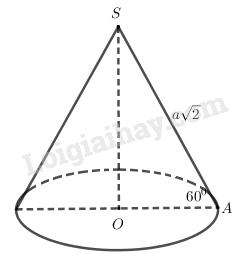
Gọi \(A\) là một điểm thuộc đường tròn đáy của hình nón.
Đường sinh \(SA = a\sqrt 2 \), góc giữa đường sinh và mặt phẳng đáy \(\widehat {SAO} = {60^0}\).
Tam giác \(SAO\) vuông tại \(O\) có:
\(OA = SA\cos {60^0} = \dfrac{{a\sqrt 2 }}{2}\); \(SO = SA\sin {60^0}\) \( = a\sqrt 2 .\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{2}\)
Diện tích xung quanh hình nón: \({S_{xq}} = \pi rl = \pi .\dfrac{{a\sqrt 2 }}{2}.a\sqrt 2 = \pi {a^2}\).
Thể tích \(V = \dfrac{1}{3}\pi {r^2}h\) \( = \dfrac{1}{3}\pi .{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2}.\dfrac{{a\sqrt 6 }}{2} = \dfrac{{\pi {a^3}\sqrt 6 }}{{12}}\).
Chọn D.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2.47 trang 66 SBT hình học 12
- Bài 2.48 trang 66 SBT hình học 12
- Bài 2.49 trang 66 SBT hình học 12
- Bài 2.45 trang 66 SBT hình học 12
- Bài 2.44 trang 66 SBT hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
