Giải vở bài tập toán lớp 9 tập 1, tập 2 Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung

Bài 18 trang 98 Vở bài tập toán 9 tập 2


Giải bài 18 trang 98 VBT toán 9 tập 2. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Tiếp tuyến A của đường tròn (O’) cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O’) tại Q...

Đề bài

Cho hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B\). Tiếp tuyến \(A\) của đường tròn \((O’)\) cắt đường tròn \((O)\) tại điểm thứ hai \(P\). Tia \(PB\) cắt đường tròn \((O’)\) tại \(Q\). Chứng minh đường thẳng \(AQ\) song song với tiếp tuyến tại \(P\) của đường tròn \((O)\).

Phương pháp giải - Xem chi tiết

Sử dụng : Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

Lời giải chi tiết

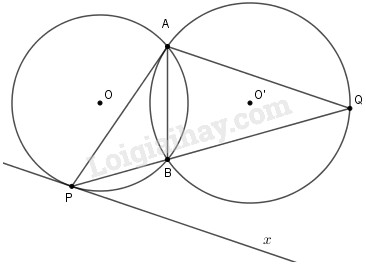
Đối với đường tròn \(\left( O \right)\) ta có

 \(\widehat {PAB} = \widehat {BPx}\) vì \(\widehat {PAB}\) là góc nội tiếp chắn cung \(PB\) và \(\widehat {BPx}\) là góc tạo bởi tiếp tuyến và dây cung \(BP\)  (1)

Đối với đường tròn \(\left( {O'} \right)\), ta có:

\(\widehat {AQB} = \widehat {PAB}\) vì \(\widehat {AQB}\) là góc nội tiếp chắn cung \(AB\) và \(\widehat {PAB}\) là góc tạo bởi tiếp tuyến và dây cung \(AB\)  (2)

Vậy từ (1) và (2) \( \Rightarrow \widehat {BPx} = \widehat {ABQ}\) nên \(AQ//Px\) vì hai góc so le trong bằng nhau.

Loigiaihay.com


Bình chọn:
4.5 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store