-
GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
- Bài 1. Tính đơn điệu của hàm số
- Bài 2. Cực trị của hàm số
- Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Bài 4. Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5. Đường tiệm cận của đồ thị hàm số
- Bài 6. Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị hàm số của một số hàm phân thức hữu tỉ
- Bài 8. Một số bài toán thường gặp về đồ thị
- Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Bài tập trắc nghiệm khách quan chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số - Toán 12 Nâng cao
-
CHƯƠNG II. HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3. Lôgarit
- Bài 4. Số e và loogarit tự nhiên
- Bài 5. Hàm số mũ và hàm số lôgarit
- Bài 6. Hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Hệ phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Bài tập trắc nghiệm khách quan chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit - Toán 12 Nâng cao
-
CHƯƠNG III. NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
- Bài 1. Nguyên hàm
- Bài 2. Một số phương pháp tìm nguyên hàm
- Bài 3. Tích phân
- Bài 4. Một số phương pháp tích phân
- Bài 5. Ứng dụng tích phân để tính diện tích hình phẳng
- Bài 6. Ứng dụng tích phân để tính thể tích vật thể
- Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
- Bài tập trắc nghiệm khách quan chương III - Nguyên hàm, tích phân và ứng dụng - Toán 12 Nâng cao
-
CHƯƠNG IV. SỐ PHỨC
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
-
HÌNH HỌC - TOÁN 12 NÂNG CAO
Câu 22 trang 214 SGK Giải tích 12 Nâng cao
Giải các phương trình sau trên C
Giải các phương trình sau trên C
LG a
z2 – 3z + 3 + i = 0
Lời giải chi tiết:
z2 – 3z + 3 + i = 0 có biệt thức là:
Δ = 32 – 4(3 + i) = -3 – 4i = (-1 + 2i )2
Nên nghiệm của nó là:
\(\left\{ \matrix{
z_1={{3 + ( - 1 + 2i)} \over 2} = 1 + i \hfill \cr
z_2={{3 - ( - 1 + 2i)} \over 2} = 2 - i \hfill \cr} \right.\)
LG b
\({z^2} - (cos\varphi + i\sin \varphi )z + i\sin \varphi \cos \varphi = 0\)
trong đó \(\varphi\) là số thực cho trước
Lời giải chi tiết:
Ta có:
\(\eqalign{
& {z^2} - (cos\varphi + i\sin \varphi )z + i\sin \varphi \cos \varphi = 0 \cr
& \Leftrightarrow {z^2} - \cos \varphi .z - i\sin \varphi .z + isin\varphi cos\varphi = 0 \cr
& \Leftrightarrow z(z - cos\varphi ) - isin\varphi (z - cos\varphi ) = 0 \cr
& \Leftrightarrow (z - cos\varphi )(z - isin\varphi ) = 0 \cr
& \Leftrightarrow \left[ \matrix{
z = \cos \varphi \hfill \cr
z = i\sin \varphi \hfill \cr} \right. \cr} \)
Vậy \(S = {\rm{\{ cos}}\varphi {\rm{;}}\,i\sin \varphi )\).
Cách khác:
Ta có biệt số
∆=(cosφ+i sinφ )2-4i sinφ.cosφ
=cos2 φ+2i.cosφ.sinφ- sin2φ-4isinφ.cosφ
= cos(2φ)-i sin(2φ)
=cos(-2φ)+i sin(-2φ)
∆ có hai căn bậc hai là: cos(-φ)+i sin(-φ) và (-cos(-φ)-i sin(-φ)
Nên phương trình có nghiệm là:
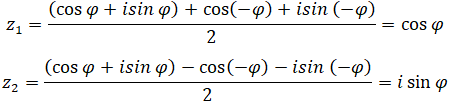
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 23 trang 214 SGK Giải tích 12 Nâng cao
- Câu 21 trang 214 SGK Giải tích 12 Nâng cao
- Câu 20 trang 214 SGK Giải tích 12 Nâng cao
- Câu 19 trang 214 SGK Giải tích 12 Nâng cao
- Câu 18 trang 214 SGK Giải tích 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
