-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Giải bài 5 trang 39 SGK Hình học lớp 12
Một hình trụ có bán kính đáy r = 5cm và có khoảng cách giữa hai đáy bằng 7 cm.
Video hướng dẫn giải
Một hình trụ có bán kính đáy \(r = 5cm\) và có khoảng cách giữa hai đáy bằng \(7 cm\).
LG a
a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên.
Phương pháp giải:
Diện tích xung quanh của hình trụ \({S_{xq}} = 2\pi rh\),
Thể tích khối trụ \(V = \pi {r^2}h\).
Với \(r;h\) lần lượt là bán kính đáy và độ dài đường cao của hình trụ.
Lời giải chi tiết:
Theo đầu bài, hình trụ có chiều cao \(h = 7 cm\) và bán kính đáy \(r = 5 cm\).
Vậy diện tích xung quanh bằng: \(S_{xq}= 2πrh = 2π.5.7= 70π\)(\(cm^2\))
Thể tích của khối trụ là: \(V = πr^2h =π.5^2.7= 175π\) (\(cm^3\))
LG b
b) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục \(3 cm\). Hãy tính diện tích của thiết diện được tạo nên.
Phương pháp giải:
Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục ta được thiết diện là một hình chữ nhật với một kích thước của hình chữ nhật bằng chiều cao hình trụ.
Sử dụng định lí Pytago để đính cạnh còn lại của hình chữ nhật sau đó tính diện tích hình chữ nhật đó.
Lời giải chi tiết:
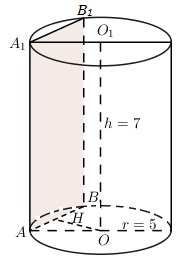
Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng \(7 cm\).
Giả sử thiết diện là \(ABB_1A_1\). Ta có \(AA_1 = 7 cm\).
Gọi \(H\) là trung điểm của \(AB\) ta có:
\(\left\{ \begin{array}{l}
OH \bot AB\\
OH \bot {A_1}A
\end{array} \right. \Rightarrow OH \bot \left( {AB{B_1}{A_1}} \right)\)
Suy ra \(d\left( {O;\left( {AB{B_1}{A_1}} \right)} \right) = OH\).
Lại có: \(O{O_1}\,{\rm{// }}(A{A_1}{B_1}B)\) nên \(OH = d\left( {O;{\rm{ }}(A{A_1}{B_1}B)} \right) = {\rm{ }}d\left( {O{O_1},(A{A_1}{B_1}B)} \right) = 3{\rm{ }}cm\)
Do tam giác \(OAH\) vuông tại \(H\) (quan hệ vuông góc giữa đường kính và dây cung) nên áp dụng định lí Pitago ta có: \(AH^2 = OA^2 – OH^2 = 25 – 9 = 16\).
\(\Rightarrow AH = 4 cm \Leftrightarrow AB = 8 cm\).
Vậy diện tích của thiết diện là: \(S=AB.AA_1=8.7=56\) (\(cm^2\)).
Loigiaihay.com
Bình luận
Chia sẻ
- Giải bài 6 trang 39 SGK Hình học lớp 12
- Giải bài 7 trang 39 SGK Hình học lớp 12
- Giải bài 8 trang 40 SGK Hình học lớp 12
- Giải bài 9 trang 40 SGK Hình học lớp 12
- Giải bài 10 trang 40 SGK Hình học lớp 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
