 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Bài 1. Khái niệm về mặt tròn xoay
Bài 1. Khái niệm về mặt tròn xoay
Giải bài 3 trang 39 SGK Hình học lớp 12
Cho hình nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm.
Video hướng dẫn giải
Cho hình nón tròn xoay có đường cao \(h = 20 cm\), bán kính đáy \(r = 25 cm\).
LG a
a) Tính diện tích xung quanh của hình nón đã cho.
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\) trong đó \(r\) là bán kính đáy và \(l\) là độ dài đường sinh của hình nón.
Lời giải chi tiết:
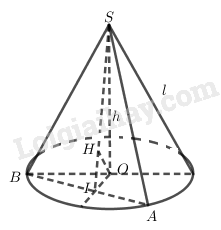
Giả sử \(SB= l\) là độ dài đường sinh, \(SO = h\) là chiều cao hình nón.
Trong tam giác vuông \(SOB\) ta có:
\(\eqalign{
& S{B^2} = S{O^2} + O{B^2} \cr&= {h^2} + {r^2} = {20^2} + {25^2} = 1025 \cr
& \Rightarrow SB = \sqrt {1025} \cr}\)
Diện tích xung quanh hình nón là:
\({S_{xq}} = \pi rl \)\(= \pi .25\sqrt {1025} \approx 2514,5\left( {c{m^2}} \right)\)
LG b
b) Tính thể tích của khối nón được tạo bởi hình nón đó.
Phương pháp giải:
Thể tích của khối nón: \(V = \dfrac{1}{3}\pi {r^2}h\) trong đó \(r\) là bán kính đáy và \(h\) là độ dài đường cao của hình nón.
Lời giải chi tiết:
Thể tích khối nón là:
\(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.25^2}.20\)\( \approx 13083,3\left( {c{m^3}} \right)\)
LG c
c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là \(12 cm\). Tính diện tích thiết diện đó.
Phương pháp giải:
Thiết diện đi qua đỉnh của hình nón là tam giác cân. Tính diện tích tam giác cân \(S = \dfrac{1}{2}ah\).
Lời giải chi tiết:
Giả sử thiết diện \(SAB\) đi qua đỉnh \(S\) cắt đường tròn đáy tại \(A\) và \(B\). Gọi \(I\) là trung điểm của dây cung \(AB\). Từ tâm \(O\) của đáy vẽ \(OH\) vuông góc với \(SI\).
Ta có \(\left\{ \matrix{
AB \bot OI \hfill \cr
AB \bot SO \hfill \cr} \right. \Rightarrow AB \bot \left( {SOI} \right) \)\(\Rightarrow AB \bot OH\)
Từ đó \(\left\{ \matrix{
OH \bot AB \hfill \cr
OH \bot SI \hfill \cr} \right. \Rightarrow OH \bot \left( {SAB} \right) \)\(\Rightarrow OH = 12cm\)
Trong tam giác vuông \(SOI\) ta có: \(\displaystyle {1 \over {O{H^2}}} = {1 \over {O{I^2}}} + {1 \over {O{S^2}}}\)
\(\eqalign{
& \Rightarrow {1 \over {O{I^2}}} = {1 \over {O{H^2}}} - {1 \over {O{S^2}}} \cr
& = {1 \over {{{12}^2}}} - {1 \over {{{20}^2}}} = {{256} \over {57600}} = {1 \over {225}} \cr
& \Rightarrow OI = 15cm \cr} \)
Xét tam giác vuông \(OAI\) ta có \(AI^2 = OA^2 – OI^2 = 25^2 – 15^2 = 20^2\)
Vậy \(AI = 20cm\)\(\Rightarrow AB = 20.2 = 40\,cm\)
Ta có: \(SI.OH = SO.OI \)\(\displaystyle \Rightarrow SI = {{SO.OI} \over {OH}} = {{20.15} \over {12}} = 25cm\)
Vậy diện tích thiết diện \(SAB\) là: \({S_{SAB}} = \displaystyle {1 \over 2}SI.AB \)\(\displaystyle= {1\over2}25.40 = 500\left( {c{m^2}} \right)\)
Loigiaihay.com












Danh sách bình luận