-
Đề thi khảo sát chất lượng đầu năm
-
Chương 1: Phép nhân và phép chia các đa thức
- Bài 1,2: Nhân đơn thức với đa thức, đa thức với đa thức
- Bài 3: Những hằng đẳng thức đáng nhớ
- Bài 4,5: Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6: Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung
- Bài 7: Phân tích đa thức thành nhân tử bằng cách dùng hằng đẳng thức
- Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9: Phối hợp nhiều phương pháp phân tích đa thức thành nhân tử
- Bài 10: Chia đơn thức cho đơn thức
- Bài 12: Chia đa thức một biến đã sắp xếp
- Bài tập ôn tập chương 1
-
Chương 2: Phân thức đại số
-
Chương 3: Phương trình bậc nhất một ẩn
-
Chương 4: Bất phương trình bậc nhất một ẩn
-
Chương 5: Tứ giác
-
Chương 6: Đa giác. Diện tích đa giác
-
Chương 7: Tam giác đồng dạng
- Bài 1,2: Định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét
- Bài 3: Tính chất đường phân giác của tam giác
- Bài 4: Hai tam giác đồng dạng
- Bài 5: Trường hợp đồng dạng thứ nhất
- Bài 6: Trường hợp đồng dạng thứ hai
- Bài 7: Trường hợp đồng dạng thứ ba
- Bài 8: Các trường hợp đồng dạng của tam giác vuông
- Bài tập ôn tập chương 7
-
Chương 8: Hình lăng trụ đứng. Hình chóp đều
Trắc nghiệm Bài 4,5,6: Hình lăng trụ đứng Toán 8
Đề bài
Các mặt bên của hình lăng trụ đứng là
-
A.
Các hình bình hành
-
B.
Các hình thang cân
-
C.
Các hình chữ nhật
-
D.
Các hình vuông
Các cạnh bên của hình lăng trụ đứng
-
A.
Song song với nhau
-
B.
Bằng nhau
-
C.
Vuông góc với hai đáy
-
D.
Có cả ba tính chất trên
Cho hình lăng trụ đứng $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình thang vuông \(\left( {\widehat A = \widehat B = {{90}^0}} \right)\) .
Có bao nhiêu cạnh song song với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(5\)
Có bao nhiêu cạnh vuông góc với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(5\)
Cho hình lăng trụ đứng $ABC.A'B'C'$ có $AB = 5cm,AC = 12cm,$$BC = 13cm.$ Có bao nhiêu mặt phẳng vuông góc với mặt phẳng $\left( {ABB'A'} \right)?$
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(3\)
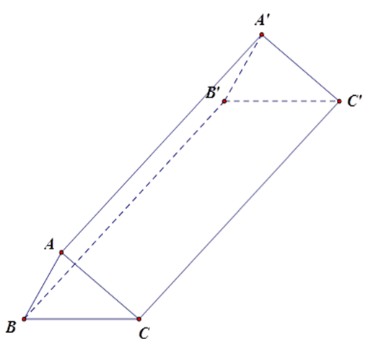
Hình lăng trụ đứng $ABC.A'B'C'$ (hình vẽ) có \(\widehat {BAC} = {90^0},AB = 6cm,AC = 8cm,{\rm{AA' = 15cm}}\) . Diện tích toàn phần của hình lăng trụ đó bằng
-
A.
\(258c{m^2}\)
-
B.
\(360c{m^2}\)
-
C.
\(456c{m^2}\)
-
D.
\(408c{m^2}\)
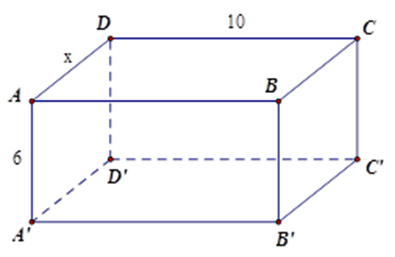
Một hình hộp chữ nhật có diện tích xung quanh bằng tổng diện tích hai đáy, chiều cao bằng $6\,cm$ . Một kích thước của đáy bằng $10\,cm$ , tính kích thước còn lại.
-
A.
\(15\,cm\)
-
B.
\(20\,cm\)
-
C.
\(25\,cm\)
-
D.
\(10\,cm\)
Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có chiều cao bằng $2cm$ , \(\widehat {BAB'} = {45^0}\) . Tính diện tích xung quanh của hình lăng trụ.
-
A.
\(15\,c{m^2}\)
-
B.
\(6\,c{m^2}\)
-
C.
\(12\,c{m^2}\)
-
D.
\(16\,c{m^2}\)
Một hình hộp chữ nhật có diện tích xung quanh bằng $120\,c{m^2}$ , chiều cao bằng $6cm$ . Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
-
A.
\(8\,cm\)
-
B.
\(7\,cm\)
-
C.
\(6\,cm\)
-
D.
\(5\,cm\)
Một hình lăng trụ đứng có đáy là hình thoi với các đường chéo của đáy bằng $16\,cm$ và $30\,cm$ . Diện tích toàn phần của hình lăng trụ bằng $1840$\(c{m^2}\). Tính chiều cao của hình lăng trụ.
-
A.
\(15\,cm\)
-
B.
\(20\,cm\)
-
C.
\(30\,cm\)
-
D.
\(25\,cm\)
Một hình hộp chữ nhật có đường chéo bằng $3\,dm$ , chiều cao $2\,dm$ , diện tích xung quanh bằng $12$\(d{m^2}\). Tính thể tích của hình hộp chữ nhật.
-
A.
\(8\,(d{m^3})\)
-
B.
\(2\,(d{m^3})\)
-
C.
\(4\,(d{m^3})\)
-
D.
\(12\,(d{m^3})\)
Tính thể tích của hình lăng trụ đứng có chiều cao $20\,{\rm{cm}}$, đáy là một tam giác vuông có các cạnh góc vuông bằng $8\,{\rm{cm}}$ và $10\,{\rm{cm}}$.
-
A.
\(800\,c{m^3}\)
-
B.
\(400\,c{m^3}\)
-
C.
\(600\,c{m^3}\)
-
D.
\(500\,c{m^3}\)
Cho lăng trụ đứng có kích thước như hình vẽ.
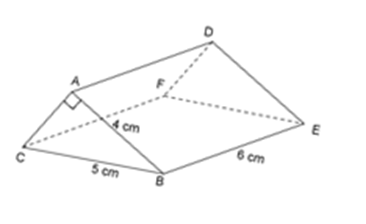
Số nào trong các số sau đây là thể tích của hình lăng trụ đứng đó?
-
A.
$20\,c{m^3}$
-
B.
$36\,c{m^3}$
-
C.
$26\,c{m^3}$
-
D.
$9\,c{m^3}$
Cho một hình lăng trụ đứng có diện tích đáy là $S$ , chiều cao là $h$ . Hỏi công thức tính thể tích hình lăng trụ đứng là gì?
-
A.
$S.h\;\;\;\;\;\;$
-
B.
\(\dfrac{1}{2}S.h\)
-
C.
$2S.h$
-
D.
$3S.h$
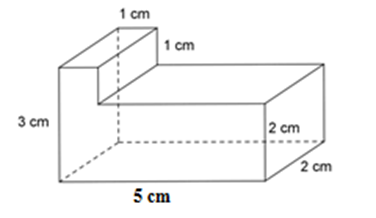
Tính thể tích của hình lăng trụ đứng sau:
-
A.
\(16\;c{m^3}\)
-
B.
\(20\;c{m^3}\)
-
C.
\(26\;c{m^3}\)
-
D.
\(22\;c{m^3}\)
Một lăng trụ đứng có đáy là hình chữ nhật có các kích thức $3$ cm, $8$ cm. Chiều cao của hình lăng trụ đứng là $2$cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đứng.
-
A.
\(48\;c{m^2},\;46\;c{m^3}\)
-
B.
\(48\;c{m^2},\;44\;c{m^3}\)
-
C.
\(46\;c{m^2},\;48\;c{m^3}\)
-
D.
\(44\;c{m^2},\;48\;c{m^3}\)
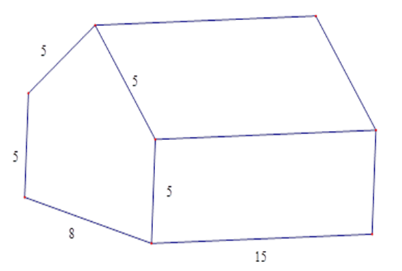
Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét .
-
A.
\(870\,{m^3}\)
-
B.
\(700\,{m^3}\)
-
C.
\(680\,{m^3}\)
-
D.
\(780\,{m^3}\)
Cho hình lăng trụ đứng $ABC.DEF$ , đáy là tam giác $ABC$ có $AB = 6\,cm,BC = 8\,cm,AC = 10\,cm$ và chiều cao của lăng trụ là $12\,cm$ .
Tam giác \(DEF\) là tam giác gì?
-
A.
Vuông tại \(E\)
-
B.
Vuông tại \(F\)
-
C.
Vuông tại \(D\)
-
D.
Đều
Diện tích xung quanh và diện tích toàn phần của lăng trụ lần lượt là:
-
A.
\(288\;c{m^2},\;336\;c{m^3}\)
-
B.
\(228\;c{m^2},\;168\;c{m^3}\)
-
C.
\(114\;c{m^2},\;336\;c{m^3}\)
-
D.
\(114\;c{m^2},\;168\;c{m^3}\)
Tính thể tích hình lăng trụ đứng.
-
A.
\(144\,c{m^3}\)
-
B.
\(822\,c{m^3}\)
-
C.
\(228\,c{m^3}\)
-
D.
\(288\,c{m^3}\)
Lời giải và đáp án
Các mặt bên của hình lăng trụ đứng là
-
A.
Các hình bình hành
-
B.
Các hình thang cân
-
C.
Các hình chữ nhật
-
D.
Các hình vuông
Đáp án : C
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Các cạnh bên của hình lăng trụ đứng
-
A.
Song song với nhau
-
B.
Bằng nhau
-
C.
Vuông góc với hai đáy
-
D.
Có cả ba tính chất trên
Đáp án : D
Hình lăng trụ đứng có các mặt bên là hình chữ nhật, các cạnh bên vuông góc với đáy nên chúng song song và bằng nhau.
Cho hình lăng trụ đứng $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình thang vuông \(\left( {\widehat A = \widehat B = {{90}^0}} \right)\) .
Có bao nhiêu cạnh song song với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(5\)
Đáp án: C
Sử dụng quan hệ song song giữa đường thẳng và mặt phẳng.
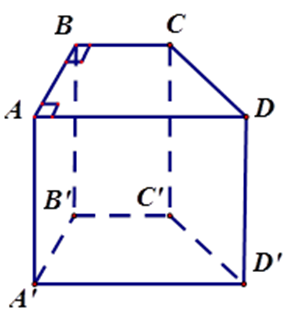
Vì $AA'{\rm{//}}BB'{\rm{//}}DD'$ và \(A'D'{\rm{//}}AD{\rm{//}}BC\) nên các đường thẳng $AA',DD',AD,A'D'$ song song với mp $\left( {BCC'B'} \right).$
Có bao nhiêu cạnh vuông góc với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(5\)
Đáp án: B
Sử dụng quan hệ vuông góc giữa đường thẳng và mặt phẳng.
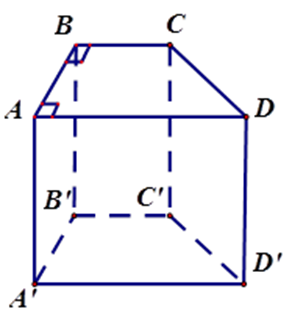
Vì \(AB \bot BC\) (do \(ABCD\) là hình thang vuông) và \(AB \bot BB'\) (tính chất lăng trụ đứng)
Nên \(AB \bot \left( {BCC'B'} \right)\) , tương tự ta có \(A'B' \bot \left( {BCC'B'} \right)\)
Do đó $AB,A'B'$ vuông góc với mp $\left( {BCC'B'} \right).$
Cho hình lăng trụ đứng $ABC.A'B'C'$ có $AB = 5cm,AC = 12cm,$$BC = 13cm.$ Có bao nhiêu mặt phẳng vuông góc với mặt phẳng $\left( {ABB'A'} \right)?$
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(3\)
Đáp án : D
+ Dùng định lý Pytago đảo để chứng minh tam giác vuông.
+ Dùng quan hệ vuông góc giữa hai mặt phẳng để tìm các cặp mặt phẳng vuông góc.
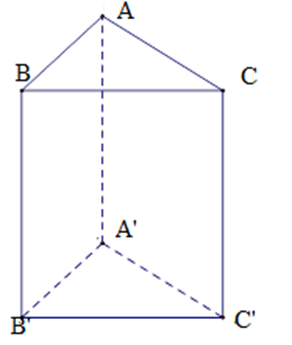
Tam giác $ABC$ có \(A{B^2} + A{C^2} = {5^2} + {12^2} = {13^2} = B{C^2}\) nên \(\Delta ABC\) vuông tại \(A\) (định lý Pytago đảo)
nên \(AC \bot AB\) . Do đó \(A'C' \bot A'B'\).
Vì $AC$ vuông góc với hai đường thẳng cắt nhau $AB$ và $AA'$ nên \(AC \bot mp(ABB'A')\)do đó \(mp(A'B'C') \bot mp(ABB'A')\).
Vậy có ba mặt phẳng vuông góc với mặt phẳng $\left( {ABB'A'} \right)$ là mp $\left( {ABC} \right)$ , mp $\left( {A'B'C'} \right),$ mp $\left( {ACC'A'} \right).$
Hình lăng trụ đứng $ABC.A'B'C'$ (hình vẽ) có \(\widehat {BAC} = {90^0},AB = 6cm,AC = 8cm,{\rm{AA' = 15cm}}\) . Diện tích toàn phần của hình lăng trụ đó bằng
-
A.
\(258c{m^2}\)
-
B.
\(360c{m^2}\)
-
C.
\(456c{m^2}\)
-
D.
\(408c{m^2}\)
Đáp án : D
Sử dụng cách tính diện tích toàn phần hình lăng trụ đứng.
Diện tích toàn phần của hình lăng trụ đứng bằng tổng của diện tích xung quanh và diện tích hai đáy
Áp dụng định lý Pytago cho tam giác \(ABC\) ta được $B{C^2} = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10\,cm$ .
Ta có chu vi đáy \({P_{ABC}} = AB + AC + BC = 6 + 8 + 10 = 24\,cm\)
Diện tích đáy \({S_{ABC}} = \dfrac{{AB.AC}}{2} = \dfrac{{6.8}}{2} = 24\,c{m^2}\) .
Diện tích xung quanh của lăng trụ đứng \({S_{xq}} = 24.15 = 360\,c{m^2}\) .
Diện tích toàn phần ${S_{tp}} = 360 + 2.24 = 408\,c{m^2}$ .
Một hình hộp chữ nhật có diện tích xung quanh bằng tổng diện tích hai đáy, chiều cao bằng $6\,cm$ . Một kích thước của đáy bằng $10\,cm$ , tính kích thước còn lại.
-
A.
\(15\,cm\)
-
B.
\(20\,cm\)
-
C.
\(25\,cm\)
-
D.
\(10\,cm\)
Đáp án : A
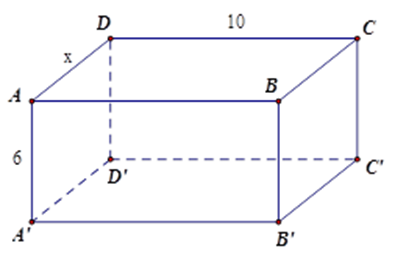
Đặt $AD = x$ .
Diện tích xung quanh bằng:
$2\left( {10 + x} \right).6\left( {c{m^2}} \right)$
Tổng diện tích hai đáy bằng $2.10x\left( {c{m^2}} \right)$
Ta có $2\left( {10 + x} \right).6{\rm{ }} = {\rm{ }}2.10x \Leftrightarrow 60 + 6x = 10x \Leftrightarrow x = 15$
Kích thước còn lại của đáy bằng $15cm$ .
Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có chiều cao bằng $2cm$ , \(\widehat {BAB'} = {45^0}\) . Tính diện tích xung quanh của hình lăng trụ.
-
A.
\(15\,c{m^2}\)
-
B.
\(6\,c{m^2}\)
-
C.
\(12\,c{m^2}\)
-
D.
\(16\,c{m^2}\)
Đáp án : C
+ Từ các điều kiện của đề bài tính chiều cao của lăng trụ
+ Sử dụng công thức tính diện tích xung quanh lăng trụ để tính toán.
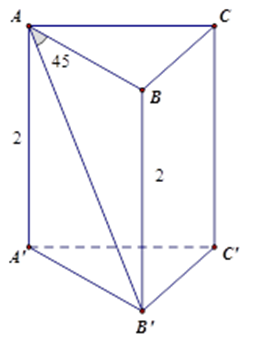
Tam giác vuông $ABB'$ có \(\widehat {BAB'} = {45^0}\) nên là tam giác vuông cân tại \(B\) nên $AB = BB' = 2cm$ .
Vì tam giác \(ABC\) đều nên chu vi đáy bằng $3AB = 3.2 = 6cm$
Diện tích xung quanh bằng $6.2 = 12\left( {c{m^2}} \right).$
Một hình hộp chữ nhật có diện tích xung quanh bằng $120\,c{m^2}$ , chiều cao bằng $6cm$ . Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
-
A.
\(8\,cm\)
-
B.
\(7\,cm\)
-
C.
\(6\,cm\)
-
D.
\(5\,cm\)
Đáp án : D
+ Sử dụng công thức thể tích và diện tích xung quanh của hình hộp chữ nhật.
+ Dùng hằng đẳng thức để biện luận theo yêu cầu đề bài.
Gọi $a$ và $b$ là các kích thước của đáy.
Ta có $V = 6ab$ nên $V$ lớn nhất \( \Leftrightarrow \) $ab$ lớn nhất
\({S_{xq}} = 120\) nên \(2\left( {a + b} \right).6 = 120\) hay \(a + b = 10\).
Ta có: \(ab = a\left( {10 - a} \right) = - {a^2} + 10a = - {\left( {a - 5} \right)^2} + 25 \le 25\).
Suy ra \(V = 6ab \le 6.25 = 150\).
Thể tích lớn nhất bằng \(150\) \({\rm{c}}{{\rm{m}}^3}\) khi \(a = b = 5\), tức là các cạnh đáy bằng $5$ cm.
Một hình lăng trụ đứng có đáy là hình thoi với các đường chéo của đáy bằng $16\,cm$ và $30\,cm$ . Diện tích toàn phần của hình lăng trụ bằng $1840$\(c{m^2}\). Tính chiều cao của hình lăng trụ.
-
A.
\(15\,cm\)
-
B.
\(20\,cm\)
-
C.
\(30\,cm\)
-
D.
\(25\,cm\)
Đáp án : B
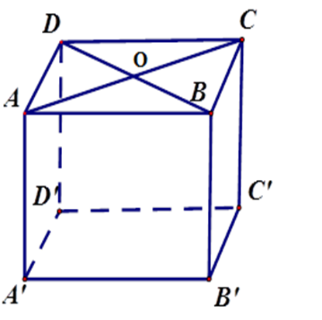
Vì đáy \(ABCD\) là hình thoi nên diện tích đáy bằng $16.30:2 = 240(c{m^2})$
Từ đó diện tích xung quanh \({S_{xq}} = 1840 - 240.2 = 1360(c{m^2})\)
Vì \(ABCD\) là hình thoi nên \(AB \bot CD;\,OD = \dfrac{{BD}}{2} = \dfrac{{30}}{2} = 15\,cm\); \(OA = \dfrac{{AC}}{2} = \dfrac{{16}}{2} = 8\,cm\) .
Nên độ dài cạnh đáy bằng \(AD = \sqrt {O{A^2} + O{D^2}} = \sqrt {{8^2} + {{15}^2}} = 17(cm)\) (định lý Pytago)
Chu vi đáy bằng \(17.4 = 68\,(cm)\)
Chiều cao hình lăng trụ bằng
$1360:68 = 20\,(cm)$ .
Một hình hộp chữ nhật có đường chéo bằng $3\,dm$ , chiều cao $2\,dm$ , diện tích xung quanh bằng $12$\(d{m^2}\). Tính thể tích của hình hộp chữ nhật.
-
A.
\(8\,(d{m^3})\)
-
B.
\(2\,(d{m^3})\)
-
C.
\(4\,(d{m^3})\)
-
D.
\(12\,(d{m^3})\)
Đáp án : C
+ Từ các dữ kiện đề bài tính các cạnh của đáy.
+ Sử dụng công thức tính thể tích hình hộp chữ nhật để tính toán.
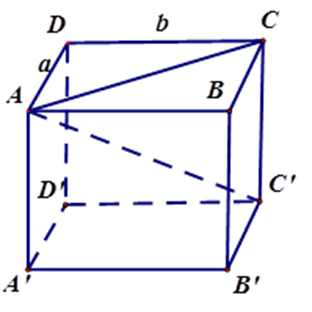
Hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AC' = 3\,dm;\,CC' = 2\,dm\) .
Xét tam giác \(ACC'\) vuông tại \(C\) , theo định lý Pytago ta có \(A{C^2} = C'{A^2} - C'{C^2} = {3^2} - {2^2} = 5\) .
Vì diện tích xung quanh là \(12\,d{m^2}\) nên chu vi đáy bằng $12:2 = 6\left( {dm} \right)$
Đặt $AD = a,{\rm{ }}DC = b$
Vì chu vi đáy là \(6\,dm \) $\Rightarrow 2\left( {a + b} \right) = 6 \Leftrightarrow a + b = 3$ (1) và ${a^2} + {b^2} = A{C^2} = 5$ (2)
(định lý Pyatgo cho tam giác vuông \(ADC\) )
Từ (1) và (2) suy ra \({a^2} + (3 - a)^2 = 5\)
Rút gọn được \({a^2} - 3a + 2 = 0\) hay \((a - 1)(a - 2) = 0\)
Giả sử \(a \ge b\) thì ta tìm được a = 2 suy ra b = 1.
Thể tích của hình hộp chữ nhật bằng \(2.1.2 = 4\,(d{m^3}).\)
Tính thể tích của hình lăng trụ đứng có chiều cao $20\,{\rm{cm}}$, đáy là một tam giác vuông có các cạnh góc vuông bằng $8\,{\rm{cm}}$ và $10\,{\rm{cm}}$.
-
A.
\(800\,c{m^3}\)
-
B.
\(400\,c{m^3}\)
-
C.
\(600\,c{m^3}\)
-
D.
\(500\,c{m^3}\)
Đáp án : A
Sử dụng công thức tính thể tích hình lăng trụ đứng \(V = S.h\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Vì đáy là tam giác vuông nên diện tích đáy \(S = \dfrac{{8.10}}{2} = 40\,cm\) .
Thể tích lăng trụ đứng là \(V = S.h = 40.20 = 800\,c{m^3}\) .
Cho lăng trụ đứng có kích thước như hình vẽ.
Số nào trong các số sau đây là thể tích của hình lăng trụ đứng đó?
-
A.
$20\,c{m^3}$
-
B.
$36\,c{m^3}$
-
C.
$26\,c{m^3}$
-
D.
$9\,c{m^3}$
Đáp án : B
Vận dụng kiến thức về định lý Py-ta-go và các công thức tính diện tích, thể tích hình lăng trụ đứng để giải bài toán
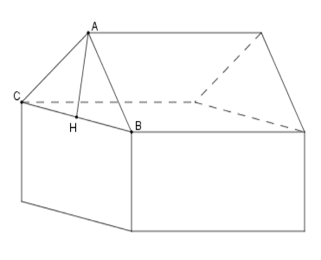
Hình lăng trụ đứng đã cho có đáy là một tam giác vuông.
Áp dụng định lý Pytago cho tam giác vuông $ABC$ , ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2} \Leftrightarrow {4^2} + A{C^2} = {5^2}\\ \Leftrightarrow A{C^2} = {5^2} - {4^2} = 9 \Rightarrow AC = 3\;cm.\end{array}\)
Vậy diện tích đáy của hình lăng trụ đứng là: \(S = {S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.4 = 6\;c{m^2}\)
Vậy thể tích của hình lăng trụ đứng là: \(V = S.h = S.BE = 6.6 = 36\;c{m^3}\)
Cho một hình lăng trụ đứng có diện tích đáy là $S$ , chiều cao là $h$ . Hỏi công thức tính thể tích hình lăng trụ đứng là gì?
-
A.
$S.h\;\;\;\;\;\;$
-
B.
\(\dfrac{1}{2}S.h\)
-
C.
$2S.h$
-
D.
$3S.h$
Đáp án : A
Công thức tính thể tích hình lăng trụ đứng là: $V = S.h$
Tính thể tích của hình lăng trụ đứng sau:
-
A.
\(16\;c{m^3}\)
-
B.
\(20\;c{m^3}\)
-
C.
\(26\;c{m^3}\)
-
D.
\(22\;c{m^3}\)
Đáp án : D
- Chia hình lăng trụ đứng thành các hình hộp chữ nhật nhỏ hơn, sau đó tính thể tích từng hình hộp chữ nhật nhỏ.
- Tính được thể tích lăng trụ đứng bằng tổng thể tích các hình hộp chữ nhật nhỏ
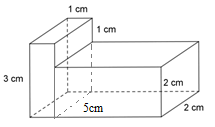
Hình lăng trụ đứng đã cho được tạo thành từ 2 hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là
\(3cm,\;\;1cm,\;\;2cm;\) hình hộp chữ nhật thứ hai có kích thước là \(2cm,\;\;4cm,\;\;2cm.\)
Thể tích hình hộp chữ nhật thứ nhất là: \({V_1} = 3.1.2 = 6\;c{m^3}\)
Thể tích hình hộp chữ nhật thứ hai là: \({V_2} = 2.4.2 = 16\;c{m^3}\)
Thể tích hình lăng trụ đứng là: \(V = {V_1} + {V_2} = 6 + 16 = 22\;c{m^3}\)
Một lăng trụ đứng có đáy là hình chữ nhật có các kích thức $3$ cm, $8$ cm. Chiều cao của hình lăng trụ đứng là $2$cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đứng.
-
A.
\(48\;c{m^2},\;46\;c{m^3}\)
-
B.
\(48\;c{m^2},\;44\;c{m^3}\)
-
C.
\(46\;c{m^2},\;48\;c{m^3}\)
-
D.
\(44\;c{m^2},\;48\;c{m^3}\)
Đáp án : D
- Áp dụng công thức tính diện tích xung quanh hình lăng trụ đứng và thể tích hình lăng trụ đứng để giải bài toán: \({S_{xq}} = 2\left( {a + b} \right)c,\;\;V = abc.\)
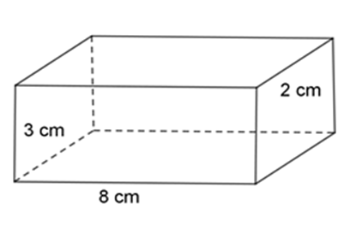
Diện tích xung quanh \({S_{xq}} = 2.(8 + 3).2 = 44\;c{m^2}\)
Thể tích của hình lăng trụ đứng là:\(V = 8.3.2 = 48\;c{m^3}\)
Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét .
-
A.
\(870\,{m^3}\)
-
B.
\(700\,{m^3}\)
-
C.
\(680\,{m^3}\)
-
D.
\(780\,{m^3}\)
Đáp án : D
+ Gọi $H$ là trung điểm $BC$. Tính $AH$ theo định lý Pytago từ đó suy ra diện tích đáy
+ Sử dụng công thức tính thể tích hình lăng trụ bằng tích diện tích đáy với chiều cao
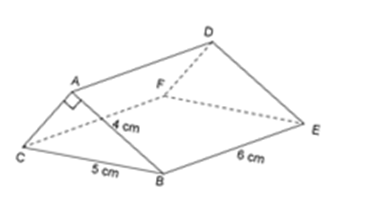
Gọi \(H\) là trung điểm \(BC \Rightarrow AH \bot BC\) . Ta có \(BH = 4;\,AB = 5\,m\)
Bằng định lí Py-ta-go ta tính được \(AH = \sqrt {A{B^2} - B{H^2}} = 3\,m\)
Diện tích đáy của hình lăng trụ bằng:
\(S = 5.8 + \dfrac{{8.3}}{2} = 52\left( {{m^2}} \right)\)
Thể tích nhà kho bằng
\(V = 52.15 = 780\left( {{m^3}} \right)\)
Cho hình lăng trụ đứng $ABC.DEF$ , đáy là tam giác $ABC$ có $AB = 6\,cm,BC = 8\,cm,AC = 10\,cm$ và chiều cao của lăng trụ là $12\,cm$ .
Tam giác \(DEF\) là tam giác gì?
-
A.
Vuông tại \(E\)
-
B.
Vuông tại \(F\)
-
C.
Vuông tại \(D\)
-
D.
Đều
Đáp án: A
- Áp dụng kiến thức định lý đảo của định lý Talet để chứng minh tam giác vuông.
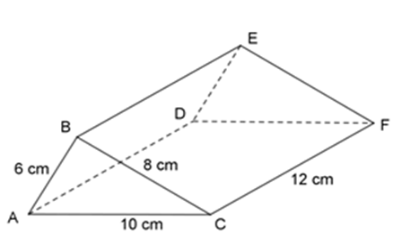
Ta có:
\(\begin{array}{l}A{B^2} + B{C^2} = {6^2} + {8^2} = 100\\A{C^2} = {10^2} = 100\\ \Rightarrow A{B^2} + B{C^2} = A{C^2}\end{array}\)
Áp dụng định lý đảo của định lý Pitago ta có tam giác $ABC$ là tam giác vuông tại $B$ .
Vì $ABC.DEF$ là hình lăng trụ đứng nên $2$ mặt đáy $ABC$ và $DEF$ song song và bằng nhau.
Suy ra tam giác $DEF$ là tam giác vuông tại $E$ .
Diện tích xung quanh và diện tích toàn phần của lăng trụ lần lượt là:
-
A.
\(288\;c{m^2},\;336\;c{m^3}\)
-
B.
\(228\;c{m^2},\;168\;c{m^3}\)
-
C.
\(114\;c{m^2},\;336\;c{m^3}\)
-
D.
\(114\;c{m^2},\;168\;c{m^3}\)
Đáp án: A
Diện tích xung quanh của hình lăng trụ $ABC.DEF$ là:
\({S_{xq}} = (6 + 8 + 10).12 = 288\;c{m^2}\)
Diện tích đáy $ABC$ của hình lăng trụ $ABC.DEF$ là:
${S_d}$ \( = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.6.8 = 24\;c{m^2}\)
Diện tích toàn phần của hình lăng trụ $ABC.DEF$ là:
${S_{tp}} = {S_{xq}} + 2.{S_d} = 288 + 2.24 = 336c{m^2}.$
Tính thể tích hình lăng trụ đứng.
-
A.
\(144\,c{m^3}\)
-
B.
\(822\,c{m^3}\)
-
C.
\(228\,c{m^3}\)
-
D.
\(288\,c{m^3}\)
Đáp án: D
Thể tích hình lăng trụ đứng $ABC.DEF$ là: $V = {S_d}.h = 24.12 = 288c{m^3}_{}$
Luyện tập và củng cố kiến thức Bài 7,8,9: Hình chóp đều, hình chóp cụt đều Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 8 Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Thể tích hình hộp chữ nhật Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1,2: Hình hộp chữ nhật Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
