Trắc nghiệm Bài 11: Hình thoi Toán 8
Đề bài
Hãy chọn câu sai.
-
A.
Tứ giác có $4$ cạnh bằng nhau là hình thoi.
-
B.
Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi.
-
C.
Hình bình hành có đường chéo là phân giác của một góc là hình thoi.
-
D.
Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
Hình thoi không có tính chất nào dưới đây?
-
A.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
-
B.
Hai đường chéo là các đường phân giác của các góc của hình thoi.
-
C.
Hai đường chéo bằng nhau.
-
D.
Hai đường chéo vuông góc với nhau.
Cho các hình sau, chọn khẳng định đúng.
-
A.
Cả ba hình đều là hình thoi.
-
B.
Hình 1 và hình 2 là hình thoi.
-
C.
Chỉ hình 1 là hình thoi.
-
D.
Cả ba hình đều không phải hình thoi.
Hình thoi có chu vi bằng $20$$cm$ thì độ dài cạnh của nó bằng
-
A.
$4\,cm$ .
-
B.
$5\,cm$ .
-
C.
$8\,cm\;\;\;\;$
-
D.
Cả A,B,C đều sai
Cho hình thoi $ABCD$ có chu vi bằng $16\,cm$ , đường cao $AH$ bằng $2\,cm$ . Tính các góc của hình thoi. Hãy chọn câu đúng.
-
A.
\(\widehat A = \widehat C = {150^o};\widehat B = \widehat D = {30^o}\).
-
B.
\(\widehat A = \widehat C = {30^o};\widehat B = \widehat D = {60^o}\).
-
C.
\(\widehat A = \widehat C = {120^o};\widehat B = \widehat D = {60^o}\).
-
D.
\(\widehat A = \widehat C = {30^o};\widehat B = \widehat D = {150^o}\).
Cho hình thang$ABCD$ . Gọi $M,N,P,Q$ lần lượt là trung điểm của$AB,BC,CD,DA$ . Hình thang $ABCD$ có thêm điều kiện gì thì $MNPQ$ là hình thoi. Hãy chọn câu đúng
-
A.
$MP = QN$ .
-
B.
\(AC \bot BD\).
-
C.
$AB = AD$ .
-
D.
$AC = BD$.
Cho hình thoi có độ dài hai đường chéo là $24\,cm$ và $10\,cm$ . Tính độ dài cạnh hình thoi.
-
A.
$12\,cm\;\;$
-
B.
\(13\,cm\)
-
C.
\(14\,cm\)
-
D.
\(15\,cm\)
Cho tam giác $ABC$ vuông ở \(A\) , trung tuyến $AM$ . Gọi $D$ là trung điểm của $AB$ , $M'$ là điểm đối xứng với $M$ qua $D$ .
Tứ giác \(AMBM'\) là hình gì?
-
A.
Hình thoi
-
B.
Hình chữ nhật
-
C.
Hình bình hành
-
D.
Hình thang
Cho \(BC = 4\,cm\) . Tính chu vi tứ giác \(AMBM'\).
-
A.
$6\,cm$
-
B.
\(9\,cm\)
-
C.
\(16\,cm\)
-
D.
\(8\,cm\)
Cho tứ giác $ABCD$ . Gọi $E,F,G$$,H$ lần lượt là trung điểm của $AB,BC,CD,DA$ . Các đường chéo $AC,BD$ của tứ giác $ABCD$ phải có điều kiện gì thì $EFGH$ là hình thoi?
-
A.
\(AC = BD\)
-
B.
\(AC \bot BD\)
-
C.
\(AB = DC\)
-
D.
\(AB{\rm{//}}DC\)
Cho tam giác $ABC$ . Trên các cạnh $AB$ và $AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $BD = CE$ . Gọi $M,N,P,Q$ thứ tự là trung điểm của $BE,CD,DE$ và $BC$ . Chọn câu đúng nhất.
-
A.
$PQ$ vuông góc với$MN$ .
-
B.
Tứ giác \(PMQN\) là hình thoi.
-
C.
Cả A, B đều đúng.
-
D.
Cả A, B đều sai.
Cho hình thoi $ABCD$ có góc $A$ tù. Biết đường cao kẻ từ đỉnh $A$ đến cạnh $CD$ chia đôi cạnh đó. Tính các góc của hình thoi.
-
A.
$\widehat B = \widehat D = {80^0},\,\,\widehat A = \widehat C = {100^0}$
-
B.
$\widehat B = \widehat D = {120^0},\,\,\widehat A = \widehat C = {60^0}$
-
C.
$\widehat B = \widehat C = {60^0},\,\,\widehat A = \widehat D = {120^0}$
-
D.
$\widehat B = \widehat D = {60^0},\,\,\widehat A = \widehat C = {120^0}$
Cho tam giác ABC đều, H là trực tâm, đường cao AD. M là điểm bất kì trên trên cạnh BC. Gọi E, F lần lượt là hình chiếu của M trên AB, AC, gọi I là trung điểm của đoạn thẳng AM. ID cắt EF tại K.
Chọn câu sai.
-
A.
M, H, K thẳng hàng
-
B.
\(\Delta IED\) đều
-
C.
Tứ giác \(EIFD\) là hình thoi
-
D.
\(ID > IF\)
Lời giải và đáp án
Hãy chọn câu sai.
-
A.
Tứ giác có $4$ cạnh bằng nhau là hình thoi.
-
B.
Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi.
-
C.
Hình bình hành có đường chéo là phân giác của một góc là hình thoi.
-
D.
Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
Đáp án : B
+ Tứ giác có bốn cạnh bằng nhau là hình thoi.
+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi..
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Nên A, C, D đúng, B sai.
Một số em khi làm chọn luôn A mà không đọc tiếp các đáp án khác vì không để ý câu hỏi chọn ý sai.
Hình thoi không có tính chất nào dưới đây?
-
A.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
-
B.
Hai đường chéo là các đường phân giác của các góc của hình thoi.
-
C.
Hai đường chéo bằng nhau.
-
D.
Hai đường chéo vuông góc với nhau.
Đáp án : C
Hình thoi có tất cả các tính chất của hình bình hành
+ Các cạnh đối song song và bằng nhau, các góc đối bằng nhau
+ Hai đường chéo giao nhau tại trung điểm mỗi đường.
Ngoài ra còn có
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc của hình thoi.
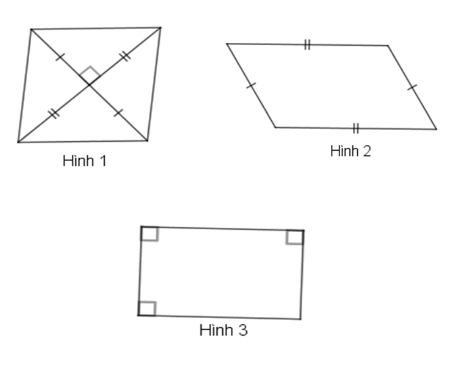
Cho các hình sau, chọn khẳng định đúng.

-
A.
Cả ba hình đều là hình thoi.
-
B.
Hình 1 và hình 2 là hình thoi.
-
C.
Chỉ hình 1 là hình thoi.
-
D.
Cả ba hình đều không phải hình thoi.
Đáp án : C
Hình 1 là hình thoi vì có hai đường chéo giao nhau tại trung điểm mỗi đường và vuông góc với nhau.
Hình 2 không là hình thoi vì bốn cạnh không bằng nhau.
Hình 3 không là hình thoi vì bốn cạnh không bằng nhau.
Hình thoi có chu vi bằng $20$$cm$ thì độ dài cạnh của nó bằng
-
A.
$4\,cm$ .
-
B.
$5\,cm$ .
-
C.
$8\,cm\;\;\;\;$
-
D.
Cả A,B,C đều sai
Đáp án : B
Sử dụng tính chất: Hình thoi có bốn cạnh bằng nhau.
Gọi cạnh của hình thoi là \(a\,\,cm\,\left( {a > 0} \right)\) .
Vì hình thoi có bốn cạnh bằng nhau nên chu vi hình thoi là \(4a = 20 \Leftrightarrow a = 5\,cm\) .
Vậy cạnh hình thoi có độ dài là \(5\,cm\) .
Cho hình thoi $ABCD$ có chu vi bằng $16\,cm$ , đường cao $AH$ bằng $2\,cm$ . Tính các góc của hình thoi. Hãy chọn câu đúng.
-
A.
\(\widehat A = \widehat C = {150^o};\widehat B = \widehat D = {30^o}\).
-
B.
\(\widehat A = \widehat C = {30^o};\widehat B = \widehat D = {60^o}\).
-
C.
\(\widehat A = \widehat C = {120^o};\widehat B = \widehat D = {60^o}\).
-
D.
\(\widehat A = \widehat C = {30^o};\widehat B = \widehat D = {150^o}\).
Đáp án : A
Bước 1: Tính cạnh hình thoi dựa vào chu vi của nó.
Bước 2: Sử dụng tính chất: “Trong tam giác vuông nếu độ dài một cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh góc vuông đó bằng \(30^\circ \)” và tính chất hình thoi để tính các góc của nó.
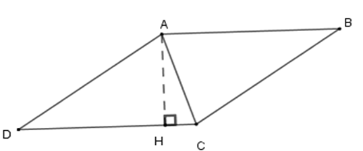
Vì chu vi hình thoi là \(16\,cm\) nên cạnh hình thoi có độ dài \(16:\,4 = 4\,cm\) . Suy ra \(AD = 4\,cm\) .
Xét tam giác \(AHD\) vuông tại \(H\) có \(AH = \dfrac{1}{2}AD \Rightarrow \widehat {ADH} = 30^\circ \) (tính chất)
Suy ra \(\widehat {DAB} = 180^\circ - \widehat {ADC} = 180^\circ - 30^\circ = 150^\circ \) (vì \(ABCD\) là hình thoi)
Nên hình thoi \(ABCD\) có \(\widehat D = \widehat B = 30^\circ ;\,\widehat A = \widehat C = 150^\circ \) (vì hai góc đối bằng nhau).
Ta có thể chứng minh tính chất: “Trong tam giác vuông nếu độ dài một cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh góc vuông đó bằng \(30^\circ \)” như sau:
Bài toán: Cho tam giác ABC vuông tại A có \(AB = \dfrac{1}{2}BC.\). Chứng minh rằng \(\widehat C = {30^0}.\)
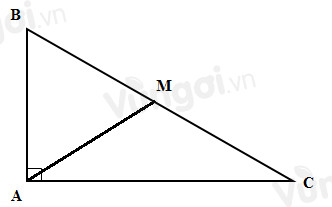
Chứng minh:
Gọi M là trung điểm của BC. Suy ra AM là đường trung tuyến ứng với cạnh huyền nên
\(AM = \dfrac{1}{2}BC\)\( \Rightarrow AM = AB = MB = MC = \dfrac{1}{2}BC\)
Suy ra tam giác MBC là tam giác đều.
Do đó, \(\widehat B = {60^0} \Rightarrow \widehat C = {90^0} - {60^0} = {30^0}.\)
Cho hình thang$ABCD$ . Gọi $M,N,P,Q$ lần lượt là trung điểm của$AB,BC,CD,DA$ . Hình thang $ABCD$ có thêm điều kiện gì thì $MNPQ$ là hình thoi. Hãy chọn câu đúng
-
A.
$MP = QN$ .
-
B.
\(AC \bot BD\).
-
C.
$AB = AD$ .
-
D.
$AC = BD$.
Đáp án : D
Bước 1: Chứng minh \(MNPQ\) là hình bình hành dựa vào tính chất đường trung bình để suy ra cặp cạnh song song và bằng nhau.
Bước 2: Để hình bình hành \(MNPQ\) là hình thoi ta cần có \(MN = MQ\) từ đó suy ra hai đường chéo của hình thang bằng nhau.
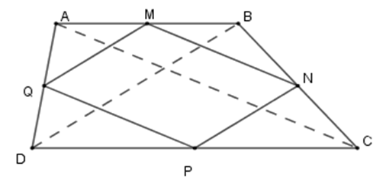
+ Xét tam giác \(ABC\) có \(MN\) là đường trung bình nên \(MN{\rm{//}}AC;\,MN = \dfrac{1}{2}AC\) (1)
Tương tự ta có \(PQ\) là đường trung bình tam giác \(ADC\) nên \(PQ{\rm{//}}AC;\,PQ = \dfrac{1}{2}AC\) (2)
Từ (1) và (2) suy ra \(MN{\rm{//}}PQ;\,MN = PQ \Rightarrow MNPQ\) là hình bình hành.
Để hình bình hành \(MNPQ\) là hình thoi ta cần có \(MN = MQ\).
Mà \(MN = \dfrac{1}{2}AC\,\left( {cmt} \right);\,MQ = \dfrac{1}{2}BD\) (do \(MQ\) là đường trung bình tam giác \(ABD\) )
Suy ra \(AC = BD\) .
Vậy để hình bình hành \(MNPQ\) là hình thoi thì \(AC = BD\).
Cho hình thoi có độ dài hai đường chéo là $24\,cm$ và $10\,cm$ . Tính độ dài cạnh hình thoi.
-
A.
$12\,cm\;\;$
-
B.
\(13\,cm\)
-
C.
\(14\,cm\)
-
D.
\(15\,cm\)
Đáp án : B
+ Ta dựa vào tính chất hình thoi để tính độ dài hai cạnh $AH,HB$
+ Tính độ dài cạnh hình thoi dựa vào định lý Pytago.
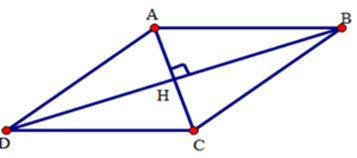
Giả sử $ABCD$ là hình thoi có hai đường chéo cắt nhau tại $H$ và $AC = 10cm,BD = 24cm.$
Do $ABCD$ là hình thoi nên:
\(AC \bot BD;AH = \dfrac{1}{2}AC \)\(= \dfrac{1}{2}.10 = 5\left( {cm} \right);\)\(\,\,HB = \dfrac{1}{2}BD = \dfrac{1}{2}.24 = 12\left( {cm} \right).\)
Xét tam giác $AHB$ vuông tại $H$ ta có: $A{B^2} = A{H^2} + H{B^2} = {5^2} + {12^2} = 25 + 144 = 169$
Suy ra $AB = 13\,cm$.
Cho tam giác $ABC$ vuông ở \(A\) , trung tuyến $AM$ . Gọi $D$ là trung điểm của $AB$ , $M'$ là điểm đối xứng với $M$ qua $D$ .
Tứ giác \(AMBM'\) là hình gì?
-
A.
Hình thoi
-
B.
Hình chữ nhật
-
C.
Hình bình hành
-
D.
Hình thang
Đáp án: A
Bước 1: Chứng minh \(MM' \bot AB\) .
Bước 2: Dùng dấu hiệu nhận biết: “Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường và vuông góc với nhau là hình thoi” để chứng minh \(AMBM'\) là hình thoi.
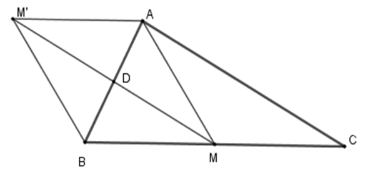
Vì \(M'\) đối xứng $M$ qua $D$ nên \(DM = DM'\) (1).
$M,D$ lần lượt là trung điểm của $BC,AB$ nên $MD$ là đường trung bình của $\Delta ABC$ . Suy ra \(MD{\rm{//}}AC\) (2).
Mặt khác $\Delta ABC$vuông ở $A$ nên \(AB \bot AC\)(2).
Từ (1) và (2) suy ra \(DM \bot AB \Rightarrow MM' \bot AB\).
Vì $D$ là trung điểm của $AB$(gt) và $D$ là trung điểm của \(MM'\) nên tứ giác $AMBM'$là hình bình hành. Mặt khác \(MM' \bot AB\)nên $AMBM'$ là hình thoi.
Cho \(BC = 4\,cm\) . Tính chu vi tứ giác \(AMBM'\).
-
A.
$6\,cm$
-
B.
\(9\,cm\)
-
C.
\(16\,cm\)
-
D.
\(8\,cm\)
Đáp án: D
Chu vi hình thoi bằng cạnh x\(4\)
Vì \(BC = 4\,cm\) nên \(BM = \dfrac{{BC}}{2} = 2\,cm\) .
Chu vi tứ giác $AMBM'$ bằng \(4.BM = 4.2 = 8\,cm\).
Cho tứ giác $ABCD$ . Gọi $E,F,G$$,H$ lần lượt là trung điểm của $AB,BC,CD,DA$ . Các đường chéo $AC,BD$ của tứ giác $ABCD$ phải có điều kiện gì thì $EFGH$ là hình thoi?
-
A.
\(AC = BD\)
-
B.
\(AC \bot BD\)
-
C.
\(AB = DC\)
-
D.
\(AB{\rm{//}}DC\)
Đáp án : A
Sử dụng dấu hiệu nhận biết hình thoi
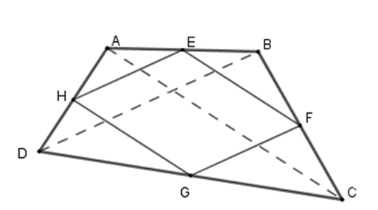
Vì $E,F$ lần lượt là trung điểm của$AB$ , $BC$ nên $EF$ là đường trung bình của $\Delta ABC$ . Suy ra \(EF{\rm{//}}AC\) và \(EF = \dfrac{1}{2}AC\) (1).
Tương tự ta có : \(HG{\rm{//}}AC\) và \(HG = \dfrac{1}{2}AC\) (2).
Từ (1) và (2) suy ra tứ giác $EFGH$ là hình bình hành.
Muốn cho tứ giác $EFGH$ là hình thoi thì nó cần phải có thêm hai cạnh kề bằng nhau.
Nên \(EH = EF \Leftrightarrow AC = BD\).
Cho tam giác $ABC$ . Trên các cạnh $AB$ và $AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $BD = CE$ . Gọi $M,N,P,Q$ thứ tự là trung điểm của $BE,CD,DE$ và $BC$ . Chọn câu đúng nhất.
-
A.
$PQ$ vuông góc với$MN$ .
-
B.
Tứ giác \(PMQN\) là hình thoi.
-
C.
Cả A, B đều đúng.
-
D.
Cả A, B đều sai.
Đáp án : C
+ Để chứng minh \(MN \bot PQ\) trước hết ta chứng minh $MNPQ$ là hình thoi dựa vào dấu hiệu tứ giác có bốn canh bằng nhau là hình thoi.
+ Ta nhận xét thấy $MN,PQ$ là hai đường chéo của hình thoi nên \(MN \bot PQ\).
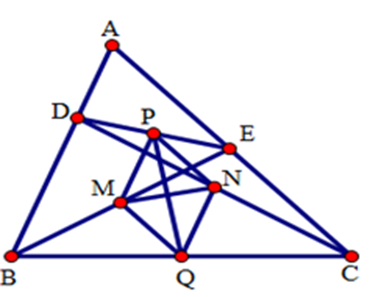
Từ giả thiết ta có $MP,NP,NQ,QM$ lần lượt là các đường trung bình của các tam giác $BDE,ECD,DCB,BEC$ . (định nghĩa đường trung bình).
Đặt $BD = CE = 2a$ .
Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:
\(MP = \dfrac{1}{2}BD = a;NQ = \dfrac{1}{2}DB = a;\)\(NP = \dfrac{1}{2}CE = a;MQ = \dfrac{1}{2}CE = a.\)
Suy ra $MN = NP = PQ = QM$ .
Tứ giác $MNPQ$ có bốn cạnh bằng nhau nên là hình thoi.
Áp dụng tính chất về đường chéo vào hình thoi $MNPQ$ ta được: \(MN \bot PQ\).
Cho hình thoi $ABCD$ có góc $A$ tù. Biết đường cao kẻ từ đỉnh $A$ đến cạnh $CD$ chia đôi cạnh đó. Tính các góc của hình thoi.
-
A.
$\widehat B = \widehat D = {80^0},\,\,\widehat A = \widehat C = {100^0}$
-
B.
$\widehat B = \widehat D = {120^0},\,\,\widehat A = \widehat C = {60^0}$
-
C.
$\widehat B = \widehat C = {60^0},\,\,\widehat A = \widehat D = {120^0}$
-
D.
$\widehat B = \widehat D = {60^0},\,\,\widehat A = \widehat C = {120^0}$
Đáp án : D
+ Ta chứng minh tam giác $ADC$ là tam giác đều từ đó suy ra số đo góc $D$
+ Ta thấy góc $C$ và góc $D$ là hai góc bù nhau nên ta suy ra số đo góc$C$ .
+ Từ đó suy ra số đo hai góc còn lại.
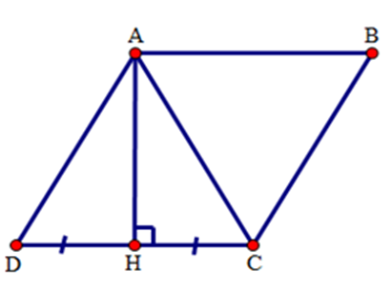
Gọi $H$ là chân đường cao kẻ từ $A$ đến cạnh $CD$ . Từ giả thiết ta có: \(AH \bot DC,CH = HD\) suy ra $AH$ là đường trung trục của đoạn $CD$ nên $AC = CD$ . (1)
Do $ABCD$ là hình thoi nên $AD = CD$ (2)
Từ (1) và (2) suy ra $AD = CD = AC$ nên tam giác $ACD$ là tam giác đều, do đó \(\widehat D = {60^0}\) .
Vì góc $A$ và góc $D$ là hai góc trong cùng phía của $AB$ // $CD$ nên chúng bù nhau hay \(\widehat A = {180^0} - {60^0} = {120^0}\).
Áp dụng tính chất về góc vào hình thoi ta được: $\widehat B = \widehat D = {60^0},\,\,\widehat A = \widehat C = {120^0}$.
Cho tam giác ABC đều, H là trực tâm, đường cao AD. M là điểm bất kì trên trên cạnh BC. Gọi E, F lần lượt là hình chiếu của M trên AB, AC, gọi I là trung điểm của đoạn thẳng AM. ID cắt EF tại K.
Chọn câu sai.
-
A.
M, H, K thẳng hàng
-
B.
\(\Delta IED\) đều
-
C.
Tứ giác \(EIFD\) là hình thoi
-
D.
\(ID > IF\)
Đáp án : D
+ Vẽ thêm $N$ là trung điểm của $AH.$
+ Ta chứng minh $MH//IN, KH//IN.$ Từ đó suy luận để có tính đúng sai của từng đáp án.
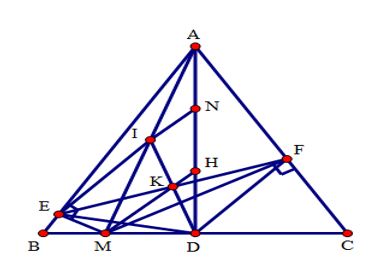
Tam giác EAM vuông tại E, EI là đường trung tuyến nên: \(EI = IM = IA = \dfrac{1}{2}AM\).
Từ EI = IA suy ra tam giác IAE cân tại I, từ đó có: \(\widehat {EIM} = 2\widehat {EAI}\) (góc ngoài của tam giác).
Chứng minh tương tự với tam giác vuông \(ADM\) ta có: \(\widehat {MID} = 2\widehat {IAD},DI = \dfrac{1}{2}AM\).
Do đó:
\(EI = DI\,\,\left( { = \dfrac{1}{2}AM} \right);\,\,\,\widehat {EID} = \widehat {EIM} + \widehat {MID} = 2\left( {\widehat {EAI} + \widehat {IAD}} \right) = 2\widehat {EAD} = {60^0}\).
Tam giác IED cân (vì EI = DI) có: \(\widehat {EID} = {60^0}\) nên là tam giác đều, từ đó EI = ED = ID.
Tương tự tam giác IDF đều suy ra: \(ID = DF = IF.\)
Do đó \(EI = ED = DF = IF.\) Suy ra tứ giác EIFD là hình thoi.
Suy ra K là trung điểm chung của EF và ID.
Gọi N là trung điểm của AH.
Tam giác ABC đều có H là trực tâm của tam giác ABC nên H cũng là trọng tâm tam giác.
Do đó \(AN = NH = HD.\)
Ta có: \(MH//IN\) (vì IN là đường trung bình của tam giác AMH) và \(KH//IN\) (vì KH là đường trung bình của tam giác DIN).
Từ H ta chỉ vẽ được một đường thẳng song song với IN (tiên đề Ơ – Clit) nên M, H, K thẳng hàng.
Vậy D sai vì \(ID = IF\)
Luyện tập và củng cố kiến thức Bài 12: Hình vuông Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 5 Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 9: Hình chữ nhật Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Đối xứng tâm Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7: Hình bình hành Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6: Đối xứng trục Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Đường trung bình của tam giác, hình thang Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2,3: Hình thang Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Tứ giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết










Danh sách bình luận