-
Đề thi khảo sát chất lượng đầu năm
-
Chương 1: Phép nhân và phép chia các đa thức
- Bài 1,2: Nhân đơn thức với đa thức, đa thức với đa thức
- Bài 3: Những hằng đẳng thức đáng nhớ
- Bài 4,5: Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6: Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung
- Bài 7: Phân tích đa thức thành nhân tử bằng cách dùng hằng đẳng thức
- Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9: Phối hợp nhiều phương pháp phân tích đa thức thành nhân tử
- Bài 10: Chia đơn thức cho đơn thức
- Bài 12: Chia đa thức một biến đã sắp xếp
- Bài tập ôn tập chương 1
-
Chương 2: Phân thức đại số
-
Chương 3: Phương trình bậc nhất một ẩn
-
Chương 4: Bất phương trình bậc nhất một ẩn
-
Chương 5: Tứ giác
-
Chương 6: Đa giác. Diện tích đa giác
-
Chương 7: Tam giác đồng dạng
- Bài 1,2: Định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét
- Bài 3: Tính chất đường phân giác của tam giác
- Bài 4: Hai tam giác đồng dạng
- Bài 5: Trường hợp đồng dạng thứ nhất
- Bài 6: Trường hợp đồng dạng thứ hai
- Bài 7: Trường hợp đồng dạng thứ ba
- Bài 8: Các trường hợp đồng dạng của tam giác vuông
- Bài tập ôn tập chương 7
-
Chương 8: Hình lăng trụ đứng. Hình chóp đều
Trắc nghiệm Bài 12: Chia đa thức một biến đã sắp xếp Toán 8
Đề bài
Phép chia đa thức \(2{x^4} - 3{x^3} + 3x - 2\) cho đa thức \({x^2} - 1\) được đa thức dư là:
-
A.
\(0\).
-
B.
\(1\).
-
C.
\(2\).
-
D.
\(10\).
Phép chia đa thức \(3{x^5} + 5{x^4} - 1\) cho đa thức \({x^2} + x + 1\) được đa thức thương là:
-
A.
\(3{x^3} - 2{x^2} - 5x + 3\).
-
B.
\(3{x^3} + 2{x^2} - 5x + 3\).
-
C.
\(3{x^3} - 2{x^2} - x + 3\).
-
D.
\(2x - 4\).
Phần dư của phép chia đa thức \({x^4} - 2{x^3} + {x^2} - 3x + 1\) cho đa thức \({x^2} + 1\) có hệ số tự do là
-
A.
\(2\).
-
B.
\(3\).
-
C.
\(1\).
-
D.
\(4\).
Biết phần dư của phép chia đa thức \(\left( {{x^5} + {x^3} + {x^2} + 2} \right)\) cho đa thức \(\left( {{x^3} + 1} \right)\) là số tự nhiên \(a\) . Chọn câu đúng.
-
A.
\(a < 2\).
-
B.
\(a > 1\).
-
C.
\(a < 0\).
-
D.
\(a \vdots 2\).
Cho các khẳng định sau:
(I): Phép chia đa thức \(3{x^3} - 2{x^2} + 5\) cho đa thức \(3x - 2\) là phép chia hết.
(II): Phép chia đa thức \(\left( {2{x^3} + 5{x^2} - 2x + 3} \right)\) cho đa thức \(\left( {2{x^2} - x + 1} \right)\) là phép chia hết
Chọn câu đúng.
-
A.
Cả (I) và (II) đều đúng.
-
B.
Cả (I) và (II) đều sai
-
C.
(I) đúng, (II) sai
-
D.
(I) sai, (II) đúng.
Kết quả của phép chia \(\left( {2{a^3} + 7a{b^2} - 7{a^2}b - 2{b^3}} \right):\left( {2a - b} \right)\) là
-
A.
\(\left( {a - b} \right)(a-2b)\).
-
B.
\({\left( {a + b} \right)^2}\).
-
C.
\(\left( {a - b} \right)(b-2a)\).
-
D.
\(a - b\).
Tìm đa thức bị chia biết đa thức chia là \(\left( {{x^2} + x + 1} \right)\), thương là \(\left( {x + 3} \right)\), dư là \(x - 2\):
-
A.
\({x^3} + 4{x^2} + 5x + 1\)
-
B.
\({x^3} - 4{x^2} + 5x + 1\)
-
C.
\({x^3} - 4{x^2} - 5x + 1\)
-
D.
\({x^3} + 4{x^2} - 5x + 1\)
Rút gọn và tính giá trị biểu thức \(A = \left( {4{x^3} + 3{x^2} - 2x} \right):\left( {{x^2} + \dfrac{3}{4}x - \dfrac{1}{2}} \right)\) tại \(x = 3\)
-
A.
\(A = 4x;A = 7\)
-
B.
\(A = 3x;A = 9\)
-
C.
\(A = 4x;A = 8\)
-
D.
\(A = 4x;A = 12\)
Xác định \(a\) để đa thức \(27{x^2} + a\) chia hết cho \(3x + 2\)
-
A.
\(a = 6\).
-
B.
\(a = 12\).
-
C.
\(a = - 12\).
-
D.
\(a = 9\).
Để đa thức \({x^4} + a{x^2} + 1\) chia hết cho \({x^2} + 2x + 1\) thì giá trị của \(a\) là
-
A.
\(a = - 2\).
-
B.
\(a = 1\).
-
C.
\(a = - 1\).
-
D.
\(a = 0\).
Có bao nhiêu giá trị của \(a\) để đa thức ${a^2}{x^3} + 3a{x^2}-6x-2a$ chia hết cho đa thức $x + 1$ .
-
A.
\(1\).
-
B.
\(2\).
-
C.
\(0\).
-
D.
Vô số
Tìm \(a\) và \(b\) để đa thức \(f\left( x \right) = {x^4} - 9{x^3} + 21{x^2} + ax + b\) chia hết cho đa thức \(g\left( x \right) = {x^2} - x - 2\)
-
A.
\(a = - 1;\,b = 30\).
-
B.
\(a = 1;\,b = 30\).
-
C.
\(a = - 1;\,b = - 30\).
-
D.
\(a = 1;\,b = - 30\).
Biết đa thức ${x^4} + a{x^2} + b$ chia hết cho ${x^2}-x + 1$ . Khi đó, khẳng định nào sau đây là đúng.
-
A.
\(a < b\)
-
B.
\(a > b\)
-
C.
\(a = b\)
-
D.
\(a = 2b\)
Cho đa thức \(f(x) = {x^4} - 3{{\rm{x}}^3} + 3{{\rm{x}}^2} + {\rm{ax}} + b\) và đa thức \(g(x) = {x^2} - 3{\rm{x}} + 4\). Biết \(f\left( x \right)\) chia hết cho \(g\left( x \right)\) . Khi đó tích \(a.b\) bằng
-
A.
\( - 12\)
-
B.
\(12\)
-
C.
\( - 6\)
-
D.
\( - 8\)
Xác định a để \(\left( {6{x^3} - 7{x^2} - x + a} \right):\left( {2x + 1} \right)\) dư \(2\)
-
A.
\( - 4\)
-
B.
\(2\)
-
C.
\( - 2\)
-
D.
\(4\)
Tìm các hằng số \(a\) và \(b\) sao cho \(\left( {{x^3} + ax + b} \right):\left( {x + 1} \right)\) dư 7 và \(\left( {{x^3} + ax + b} \right):\left( {x - 3} \right)\) dư \(\left( { - 5} \right)\)
-
A.
\(a = 10,b = 2\)
-
B.
\(a = 10,b = - 2\)
-
C.
\(a = - 10,b = - 2\)
-
D.
\(a = - 10,b = 2\)
Có bao nhiêu số nguyên \(x\) để giá trị của đa thức \(A = 2{x^3} - 3{x^2} + 2x + 2\) chia hết cho giá trị của đa thức \(B = {x^2} + 1\)
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(1\)
Phần dư của phép chia đa thức \({\left( {{x^2} + 3x + 2} \right)^5} + {\left( {{x^2} - 4x - 4} \right)^5} - 1\) cho đa thức \(x + 1\) là
-
A.
\(3\)
-
B.
\(2\)
-
C.
\(0\)
-
D.
\(1\)
\(P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}\). Tìm \(n \in Z\) để \(P \in Z\).
-
A.
\(n \in \left\{ {0,2} \right\}\)
-
B.
\(n \in \left\{ { - 1,1} \right\}\)
-
C.
\(n \in \left\{ { - 1;2} \right\}\)
-
D.
\(n \in \left\{ { - 2,0} \right\}\)
Lời giải và đáp án
Phép chia đa thức \(2{x^4} - 3{x^3} + 3x - 2\) cho đa thức \({x^2} - 1\) được đa thức dư là:
-
A.
\(0\).
-
B.
\(1\).
-
C.
\(2\).
-
D.
\(10\).
Đáp án : A
Vậy đa thức dư là \(R = 0\) .
Một số em khi thực hiện phép chia có thể nhầm dấu khi thực hiện các phép trừ các đa thức dẫn đến sai đáp án.
Phép chia đa thức \(3{x^5} + 5{x^4} - 1\) cho đa thức \({x^2} + x + 1\) được đa thức thương là:
-
A.
\(3{x^3} - 2{x^2} - 5x + 3\).
-
B.
\(3{x^3} + 2{x^2} - 5x + 3\).
-
C.
\(3{x^3} - 2{x^2} - x + 3\).
-
D.
\(2x - 4\).
Đáp án : B
Đa thức thương là $3{x^3} + 2{x^2} - 5x + 3$ .
Phần dư của phép chia đa thức \({x^4} - 2{x^3} + {x^2} - 3x + 1\) cho đa thức \({x^2} + 1\) có hệ số tự do là
-
A.
\(2\).
-
B.
\(3\).
-
C.
\(1\).
-
D.
\(4\).
Đáp án : C
Đa thức dư là \( - x + 1\) có hệ số tự do là \(1\) .
Biết phần dư của phép chia đa thức \(\left( {{x^5} + {x^3} + {x^2} + 2} \right)\) cho đa thức \(\left( {{x^3} + 1} \right)\) là số tự nhiên \(a\) . Chọn câu đúng.
-
A.
\(a < 2\).
-
B.
\(a > 1\).
-
C.
\(a < 0\).
-
D.
\(a \vdots 2\).
Đáp án : A
Phần dư của phép chia là \(a = 1 < 2\)
Một số em sai ở phép trừ cuối \(\left( {{x^3} + 2} \right) - \left( {{x^3} + 1} \right) = {x^3} + 2 - {x^3} + 1 = 3\) do không đổi dấu khi phá ngoặc nên dẫn đến chọn sai đáp án.
Cho các khẳng định sau:
(I): Phép chia đa thức \(3{x^3} - 2{x^2} + 5\) cho đa thức \(3x - 2\) là phép chia hết.
(II): Phép chia đa thức \(\left( {2{x^3} + 5{x^2} - 2x + 3} \right)\) cho đa thức \(\left( {2{x^2} - x + 1} \right)\) là phép chia hết
Chọn câu đúng.
-
A.
Cả (I) và (II) đều đúng.
-
B.
Cả (I) và (II) đều sai
-
C.
(I) đúng, (II) sai
-
D.
(I) sai, (II) đúng.
Đáp án : D
Ta có
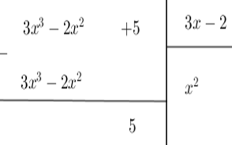
Vì phần dư \(R = 5 \ne 0\) nên phép chia đa thức \(3{x^3} - 2{x^2} + 5\) cho đa thức \(3x - 2\) là phép chia có dư. Do đó (I) sai.
Lại có
Nhận thấy phần dư \(R = 0\) nên phép chia đa thức \(\left( {2{x^3} + 5{x^2} - 2x + 3} \right)\) cho đa thức \(\left( {2{x^2} - x + 1} \right)\) là phép chia hết. Do đó (II) đúng.
Kết quả của phép chia \(\left( {2{a^3} + 7a{b^2} - 7{a^2}b - 2{b^3}} \right):\left( {2a - b} \right)\) là
-
A.
\(\left( {a - b} \right)(a-2b)\).
-
B.
\({\left( {a + b} \right)^2}\).
-
C.
\(\left( {a - b} \right)(b-2a)\).
-
D.
\(a - b\).
Đáp án : A
Phân tích đa thức bị chia thành nhân tử rồi thực hiện phép chia.
Ta có \(2{a^3} + 7a{b^2} - 7{a^2}b - 2{b^3}\)\( = 2\left( {{a^3} - {b^3}} \right) - 7ab\left( {a - b} \right) \)\(= 2\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right) - 7ab\left( {a - b} \right)\)
\( = \left( {a - b} \right)\left( {2{a^2} - ab - 4ab + 2{b^2}} \right) = \left( {a - b} \right)\left[ {a\left( {2a - b} \right) - 2b\left( {2a - b} \right)} \right]\)
\( = \left( {a - b} \right)\left( {2a - b} \right)\left( {a - 2b} \right)\)
Nên \(\left( {2{a^3} + 7a{b^2} - 7{a^2}b - 2{b^3}} \right):\left( {2a - b} \right)\)\( = {\left( {a - b} \right)}.(2a-b).\left( {a - 2b} \right):\left( {2a - b} \right) = \left( {a - b} \right)(a-2b)\) .
Tìm đa thức bị chia biết đa thức chia là \(\left( {{x^2} + x + 1} \right)\), thương là \(\left( {x + 3} \right)\), dư là \(x - 2\):
-
A.
\({x^3} + 4{x^2} + 5x + 1\)
-
B.
\({x^3} - 4{x^2} + 5x + 1\)
-
C.
\({x^3} - 4{x^2} - 5x + 1\)
-
D.
\({x^3} + 4{x^2} - 5x + 1\)
Đáp án : A
- Ta nhân đa thức thương với đa thức chia rồi cộng với số dư, ta thu được đa thức bị chia cần tìm.
Đa thức bị chia cần tìm là:
\(\left( {{x^2} + x + 1} \right)\left( {x + 3} \right) + x - 2 = {x^2}.x + 3{x^2} + x.x + 3x + x + 3 + x - 2 = {x^3} + 4{x^2} + 5x + 1\)
Rút gọn và tính giá trị biểu thức \(A = \left( {4{x^3} + 3{x^2} - 2x} \right):\left( {{x^2} + \dfrac{3}{4}x - \dfrac{1}{2}} \right)\) tại \(x = 3\)
-
A.
\(A = 4x;A = 7\)
-
B.
\(A = 3x;A = 9\)
-
C.
\(A = 4x;A = 8\)
-
D.
\(A = 4x;A = 12\)
Đáp án : D
- Đặt phép chia.
- Ta thu được biểu thức rút gọn, ta thay giá trị biến đã biết vào biểu thức rút gọn để tìm được giá trị biểu thức.
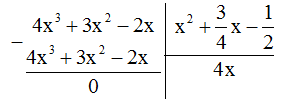
Tại \(x = 3\) , ta có: \(A = 4x = 4.3 = 12\)
Xác định \(a\) để đa thức \(27{x^2} + a\) chia hết cho \(3x + 2\)
-
A.
\(a = 6\).
-
B.
\(a = 12\).
-
C.
\(a = - 12\).
-
D.
\(a = 9\).
Đáp án : C
+ Sử dụng cách chia đa thức một biến đã sắp xếp.
+ Sử dụng nhận xét: Nếu phép chia có phần dư \(R = 0\) thì phép chia đó là phép chia hết.
Ta có
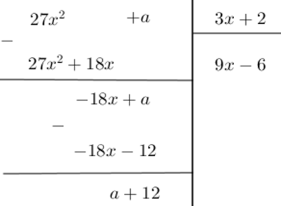
Suy ra \(27{x^2} + a = \left( {3x + 2} \right)\left( {9x - 6} \right) + a + 12\). Để phép chia trên là phép chia hết thì \(R = a + 12 = 0 \Leftrightarrow a = - 12\) .
Một số em trừ sai ở bước cuối dẫn đến ra phần dư là \(a - 12\) . Do đó ra đáp án B sai.
Để đa thức \({x^4} + a{x^2} + 1\) chia hết cho \({x^2} + 2x + 1\) thì giá trị của \(a\) là
-
A.
\(a = - 2\).
-
B.
\(a = 1\).
-
C.
\(a = - 1\).
-
D.
\(a = 0\).
Đáp án : A
+ Sử dụng cách chia đa thức một biến đã sắp xếp.
+ Sử dụng nhận xét: Nếu phép chia có phần dư \(R = 0\) thì phép chia đó là phép chia hết.
Chú ý: \(Ax + B = 0\) với \(\forall x \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) .
Ta có
Phần dư của phép chia đa thức \({x^4} + a{x^2} + 1\) chia hết cho\({x^2} + 2x + 1\) là \(R = \left( { - 2a - 4} \right)x - a - 2\) .
Để phép chia trên là phép chia hết thì \(R = 0 \Leftrightarrow \left( { - 2a - 4} \right)x - a - 2 = 0\) với mọi $x$
\( \Leftrightarrow \left\{ \begin{array}{l} - 2a - 4 = 0\\ - a - 2 = 0\end{array} \right. \Leftrightarrow a = - 2\) .
Có bao nhiêu giá trị của \(a\) để đa thức ${a^2}{x^3} + 3a{x^2}-6x-2a$ chia hết cho đa thức $x + 1$ .
-
A.
\(1\).
-
B.
\(2\).
-
C.
\(0\).
-
D.
Vô số
Đáp án : B
+ Sử dụng cách chia đa thức một biến đã sắp xếp.
+ Sử dụng nhận xét: Nếu phép chia có phần dư \(R = 0\) thì phép chia đó là phép chia hết.
Ta có
Phần dư của phép chia trên là \(R = - {a^2} + a + 6\) . Để phép chia trên là phép chia hết thì \(R = 0 \Leftrightarrow - {a^2} + a + 6 = 0\)
\( \Leftrightarrow - {a^2} - 2a + 3a + 6 = 0 \)\(\Leftrightarrow - a\left( {a + 2} \right) + 3\left( {a + 2} \right) = 0\) \( \Leftrightarrow \left( {a + 2} \right)\left( { - a + 3} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}a = - 2\\a = 3\end{array} \right.\)
Vậy có hai giá trị của $a$ thỏa mãn điều kiện đề bài $a = - 2;a = 3$ .
Một số em tính sai ở bước cuối của phép chia dẫn đến phần dư là \(R = {a^2} + a + 6\) . Do đó chọn sai đáp án.
Tìm \(a\) và \(b\) để đa thức \(f\left( x \right) = {x^4} - 9{x^3} + 21{x^2} + ax + b\) chia hết cho đa thức \(g\left( x \right) = {x^2} - x - 2\)
-
A.
\(a = - 1;\,b = 30\).
-
B.
\(a = 1;\,b = 30\).
-
C.
\(a = - 1;\,b = - 30\).
-
D.
\(a = 1;\,b = - 30\).
Đáp án : D
+ Sử dụng cách chia đa thức một biến đã sắp xếp.
+ Sử dụng nhận xét: Nếu phép chia có phần dư \(R = 0\) thì phép chia đó là phép chia hết.
Chú ý: \(Ax + B = 0\) với \(\forall x \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) .
Ta có
Phần dư của phép chia \(f\left( x \right)\) cho \(g\left( x \right)\) là \(R = \left( {a - 1} \right)x + b + 30\)
Để phép chia trên là phép chia hết thì \(R = 0\) với \(\forall x\) \( \Leftrightarrow \left( {a - 1} \right)x + b + 30 = 0\) với \(\forall x\)
\( \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\b + 30 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 30\end{array} \right.\) . Vậy \(a = 1;\,b = - 30\).
Một số em tính sai ở bước cuối khi thực hiện phép chia dẫn đến phần dư là \(R = \left( {a - 1} \right)x + b - 30\) do đó ra sai đáp án.
Biết đa thức ${x^4} + a{x^2} + b$ chia hết cho ${x^2}-x + 1$ . Khi đó, khẳng định nào sau đây là đúng.
-
A.
\(a < b\)
-
B.
\(a > b\)
-
C.
\(a = b\)
-
D.
\(a = 2b\)
Đáp án : C
+ Sử dụng cách chia đa thức một biến đã sắp xếp.
+ Sử dụng nhận xét: Nếu phép chia có phần dư \(R = 0\) thì phép chia đó là phép chia hết.
Chú ý: \(Ax + B = 0\) với \(\forall x \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) .
Ta có
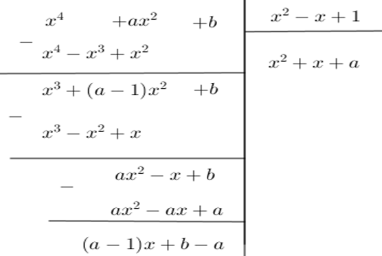
Phần dư của phép chia là \(R = \left( {a - 1} \right)x + b - a\) . Để phép chia trên là phép chia hết thì $R = 0,\,\forall x \Leftrightarrow \left( {a - 1} \right)x + b - a = 0,\,\forall x$ \( \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\b - a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 1\end{array} \right. \Leftrightarrow a = b\) .
Một số em có thể ra phần dư sai \(R = \left( {a + 1} \right)x + b + a\) (do nhầm dấu) dẫn đến sai kết quả.
Cho đa thức \(f(x) = {x^4} - 3{{\rm{x}}^3} + 3{{\rm{x}}^2} + {\rm{ax}} + b\) và đa thức \(g(x) = {x^2} - 3{\rm{x}} + 4\). Biết \(f\left( x \right)\) chia hết cho \(g\left( x \right)\) . Khi đó tích \(a.b\) bằng
-
A.
\( - 12\)
-
B.
\(12\)
-
C.
\( - 6\)
-
D.
\( - 8\)
Đáp án : A
+ Sử dụng cách chia đa thức một biến đã sắp xếp.
+ Sử dụng nhận xét: Nếu phép chia có phần dư \(R = 0\) thì phép chia đó là phép chia hết.
Chú ý: \(Ax + B = 0\) với \(\forall x \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) .
Ta có
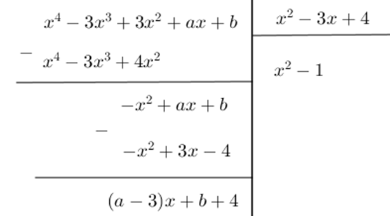
Phần dư của phép chia $f\left( x \right)$ cho \(g\left( x \right)\) là \(R = \left( {a - 3} \right)x + b + 4\) . Để phép chia trên là phép chia hết thì \(R = 0,\forall x \Leftrightarrow \left( {a - 3} \right)x + b + 4 = 0,\,\forall x \Leftrightarrow \left\{ \begin{array}{l}a - 3 = 0\\b + 4 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 4\end{array} \right. \Rightarrow ab = - 12\) .
Một số em có thể nhân nhầm dấu ở bước cuối dẫn đến sai đáp án.
Xác định a để \(\left( {6{x^3} - 7{x^2} - x + a} \right):\left( {2x + 1} \right)\) dư \(2\)
-
A.
\( - 4\)
-
B.
\(2\)
-
C.
\( - 2\)
-
D.
\(4\)
Đáp án : D
- Đặt phép chia.
- Để phép chia hết thì số dư cuối cùng phải bằng \(0\), từ đó ta tìm ra \(a\) và \(b\).
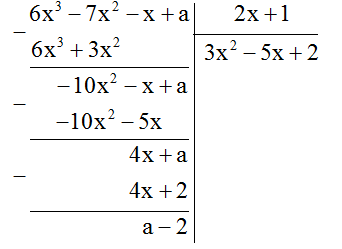
Để \(6{x^3} - 7{x^2} - x + a\) chia \(2x + 1\) dư \(2\) thì \(a - 2 = 2 \Leftrightarrow a = 4\).
Tìm các hằng số \(a\) và \(b\) sao cho \(\left( {{x^3} + ax + b} \right):\left( {x + 1} \right)\) dư 7 và \(\left( {{x^3} + ax + b} \right):\left( {x - 3} \right)\) dư \(\left( { - 5} \right)\)
-
A.
\(a = 10,b = 2\)
-
B.
\(a = 10,b = - 2\)
-
C.
\(a = - 10,b = - 2\)
-
D.
\(a = - 10,b = 2\)
Đáp án : C
- Đặt phép chia.
- Để phép chia có dư theo điều kiện đề bài thì số dư cuối cùng phải bằng số dư đề bài cho. Từ đó ta được phương trình thứ nhất.
- Thực hiện tương tự, được phương trình thứ hai. Lập hệ phương trình, giải hệ thu được giá trị của a và b.
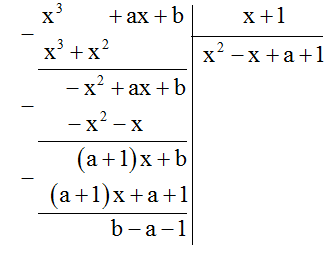
Để \({x^3} + ax + b\) chia cho \(x + 1\) dư \(7\) thì \(b - a - 1 = 7 \Leftrightarrow - a + b = 8\;(1)\)
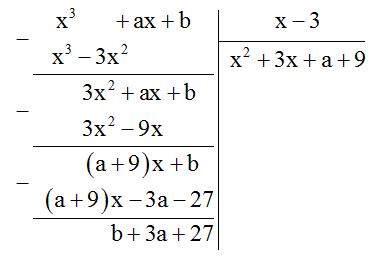
Để \({x^3} + ax + b\) chia cho \(x - 3\) dư \( - 5\) thì \(b + 3a + 27 = -5 \Leftrightarrow 3a + b = - 32\;(2)\)
Từ (1) và (2) ta có hệ \(\left\{ \begin{array}{l} - a + b = 8\\3a + b = - 32\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 10\\b = - 2\end{array} \right.\)
Vậy \(a = - 10,b = - 2\).
Có bao nhiêu số nguyên \(x\) để giá trị của đa thức \(A = 2{x^3} - 3{x^2} + 2x + 2\) chia hết cho giá trị của đa thức \(B = {x^2} + 1\)
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(1\)
Đáp án : A
- Đặt phép chia.
- Để thỏa mãn điều kiện của đề bài thì số dư cuối cùng phải chia hết cho số chia. Suy ra, số chia là ước của số dư cuối cùng.
- Lập bảng thử chọn để chọn ra giá trị của \(n\) thỏa mãn.
Ta có \(A:B\)
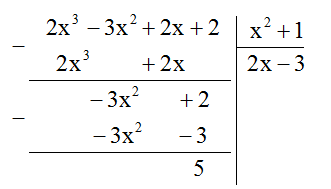
Để giá trị của đa thức \(A = 2{x^3} - 3{x^2} + 2x + 2\) chia hết cho giá trị của đa thức \(B = {x^2} + 1\) thì \(5\,\, \vdots \,\,\left( {{x^2} + 1} \right)\)
Hay \(\left( {{x^2} + 1} \right) \in U\left( 5 \right) = \left\{ { - 1;1; - 5;5} \right\}\)
+) \({x^2} + 1 = - 1 \Leftrightarrow {x^2} = - 2\left( {VL} \right)\)
+) \({x^2} + 1 = 1 \Leftrightarrow {x^2} = 0 \Leftrightarrow x = 0\left( {tm} \right)\)
+) \({x^2} + 1 = - 5 \Leftrightarrow {x^2} = - 6\left( {VL} \right)\)
+) \({x^2} + 1 = 5 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\left( {tm} \right)\)
Vậy có 3 giá trị của \(x\) thỏa mãn đề bài là \(x = 0;x = - 2;x = 2.\)
Phần dư của phép chia đa thức \({\left( {{x^2} + 3x + 2} \right)^5} + {\left( {{x^2} - 4x - 4} \right)^5} - 1\) cho đa thức \(x + 1\) là
-
A.
\(3\)
-
B.
\(2\)
-
C.
\(0\)
-
D.
\(1\)
Đáp án : C
Sử dụng \(P\left( x \right) = Q\left( x \right).\left( {x + 1} \right) + R\)
Thay \(x = - 1\) vào biểu thức trên ta nhận được phần dư \(r.\)
Ta có đa thức chia \(\left( {x + 1} \right)\) nên phần dư là một hằng số
Gọi thương là \(Q\left( x \right)\) và dư \(r\). Khi đó với mọi \(x\) ta có \({\left( {{x^2} + 3x + 2} \right)^5} + {\left( {{x^2} - 4x - 4} \right)^5} - 1 = Q\left( x \right)\left( {x + 1} \right) + r\) (1)
Thay \(x = - 1\) vào (1) ta được \({\left( {{{\left( { - 1} \right)}^2} + 3.\left( { - 1} \right) + 2} \right)^5} + {\left( {{{\left( { - 1} \right)}^2} - 4\left( { - 1} \right) - 4} \right)^5} - 1 = Q\left( x \right).\left( { - 1 + 1} \right) + r\)
\(r = {0^5} + {1^5} - 1 \Leftrightarrow r = 0\)
Vậy phần dư của phép chia là \(r = 0.\)
\(P = \dfrac{{2{n^3} - 3{n^2} + 3n - 1}}{{n - 1}}\). Tìm \(n \in Z\) để \(P \in Z\).
-
A.
\(n \in \left\{ {0,2} \right\}\)
-
B.
\(n \in \left\{ { - 1,1} \right\}\)
-
C.
\(n \in \left\{ { - 1;2} \right\}\)
-
D.
\(n \in \left\{ { - 2,0} \right\}\)
Đáp án : A
- Đặt phép chia.
- Để thỏa mãn điều kiện của đề bài thì số dư cuối cùng phải chia hết cho số chia. Suy ra, số chia là ước của số dư cuối cùng.
- Lập bảng thử chọn để chọn ra giá trị của \(n\)thỏa mãn.
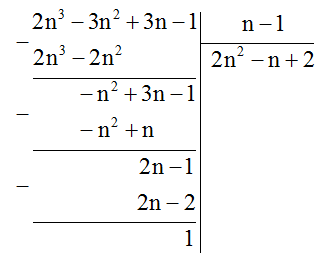
\(2{n^3} - 3{n^2} + 3n - 1 = \left( {2{n^2} - n + 2} \right)\left( {n - 1} \right) + 1\)
Để \(2{n^3} - 3{n^2} + 3n - 1\) chia hết cho \(n - 1\) thì \(1\) chia hết cho \(n - 1\).
\( \Rightarrow \left( {n - 1} \right) \in \left\{ {1, - 1} \right\}\)
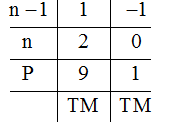
Vậy \(n \in \left\{ {0,2} \right\}\) để \(P \in Z\).
Luyện tập và củng cố kiến thức Bài tập ôn tập chương 1 Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 10: Chia đơn thức cho đơn thức Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 9: Phối hợp nhiều phương pháp phân tích đa thức thành nhân tử Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7: Phân tích đa thức thành nhân tử bằng cách dùng hằng đẳng thức Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6: Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4,5: Những hằng đẳng thức đáng nhớ (tiếp) Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Những hằng đẳng thức đáng nhớ Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1,2: Nhân đơn thức với đa thức, đa thức với đa thức Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Danh sách bình luận