-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Lý thuyết mặt cầu
Lý thuyết mặt câu đầy đủ, ngắn gọn dễ hiểu
1. Định nghĩa:
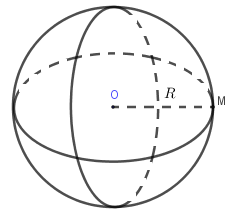
Tập hợp các điểm trong không gian cách điểm \(O\) cố định một khoảng không đổi \(r (r>0)\) được gọi là một mặt cầu tâm \(O\) bán kính \(r\).
Kí hiệu: \(S\left( {O;R} \right) = \left\{ {\left. M \right|OM = R} \right\}\)
* Cho mặt cầu \(S(O;r)\) và điểm \(A\) trong không gian.
- Nếu \(OA = r\) thì điểm \(A\) nằm trên mặt cầu
- Nếu \(OA < r\) thì điểm \(A\) nằm trong mặt cầu.
- Nếu \(OA > r\) thì điểm \(A\) nằm ngoài mặt cầu.
2. Tính chất:
Nếu điểm \(A\) ngoài mặt cầu \(S(O; r)\) thì:
- Qua \(A\) có vô số tiếp tuyến với mặt cầu.
- Độ dài các đoạn thẳng nối \(A\) với các tiếp điểm đều bằng nhau.
- Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
3. Giao của mặt cầu với mặt phẳng
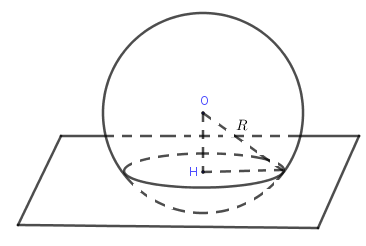
Cho mặt cầu \(\left( S \right)\) tâm \(O\), bán kính \(R\) và mặt phẳng \(\left( P \right)\), gọi \(H\) là hình chiếu của \(O\) trên \(\left( P \right)\).
+ Nếu \(OH < R\) thì \(\left( S \right)\) cắt \(\left( P \right)\) theo đường tròn tâm \(H\) và bán kình \(r = \sqrt {{R^2} - O{H^2}} \).
+ Nếu \(OH = R\) thì \(\left( S \right)\) tiếp xúc \(\left( P \right)\) tại tiếp điểm \(H\).
+ Nếu \(OH > R\) thì \(\left( S \right)\) và \(\left( P \right)\) không có điểm chung.
Đặc biệt: Nếu \(OH = 0\left( {O \equiv H} \right)\) thì đường tròn giao tuyến của \(\left( P \right)\) và \(\left( S \right)\) được gọi là đường tròn lớn, \(\left( P \right)\) được gọi là mặt phẳng kính.
4. Giao của mặt cầu với đường thẳng.
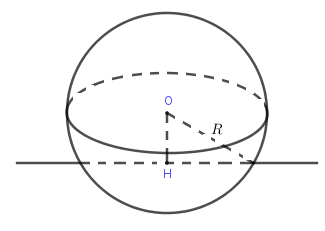
Cho mặt cầu \(\left( S \right)\) tâm \(O\), bán kính \(R\) và đường thẳng \(d\), gọi \(H\) là hình chiếu của \(O\) trên \(d\).
+ Nếu \(OH < R\) thì \(\left( S \right)\) cắt \(d\) tại \(2\) điểm phân biệt.
+ Nếu \(OH = R\) thì \(\left( S \right)\) cắt \(d\) tại một điểm duy nhất \(H\). (\(d\) là tiếp tuyến với mặt cầu, \(H\) là tiếp điểm)
+ Nếu \(OH > R\) thì \(\left( S \right)\) và \(d\) không có điểm chung.
5. Tiếp tuyến với mặt cầu (Đọc thêm)
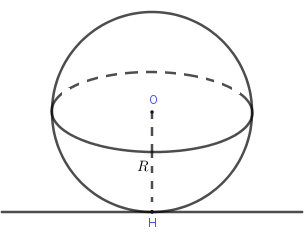
- Qua một điểm nằm trong mặt cầu không vẽ được tiếp tuyến nào với mặt cầu.
- Qua một điểm nằm trên mặt cầu vẽ được vô số tiếp tuyến với mặt cầu tại điểm đó. Tập hợp các tiếp tuyến chính là mặt phẳng tiếp diện của mặt cầu.
- Qua một điểm nằm ngoài mặt cầu vẽ được vô số tiếp tuyến với mặt cầu. Tập hợp các tiếp điểm với mặt cầu là đường tròn nằm trên mặt cầu.
6. Công thức diện tích mặt cầu và thể tích hình cầu
Bình luận
Chia sẻ
- Trả lời câu hỏi 1 trang 43 SGK Hình học 12
- Trả lời câu hỏi 2 trang 45 SGK Hình học 12
- Trả lời câu hỏi 4 trang 48 SGK Hình học 12
- Trả lời câu hỏi 3 trang 48 SGK Hình học 12
- Giải bài 1 trang 49 SGK Hình học lớp 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
