Giải bài 7 trang 49 SGK Hình học lớp 12
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, AD = c.
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AA' = a, AB = b, AD = c\).
LG a
a) Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.
Phương pháp giải:
Xác định tâm và bán kính của hình hộp dựa vào tính chất các đường chéo của hình hộp thì bằng nhau
Lời giải chi tiết:
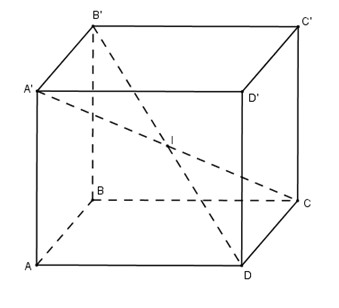
Trong hình hộp chữ nhật, bốn đường chéo \(\displaystyle AC', BD', CA' và DB'\) cắt nhau tại điểm \(\displaystyle I\) là trung điểm của mỗi đường.
Vì \(\displaystyle 4\) đường chéo trong hình hộp chữ nhật bằng nhau, nên điểm \(\displaystyle I\) cách đều \(\displaystyle 8\) đỉnh của hình hộp chữ nhật. Nó là tâm của mặt cầu ngoại tiếp hình hộp.
Vì \(\displaystyle AB = b, AD = c, AA' = a\) nên bán kính mặt cầu \(\displaystyle R = {1 \over 2}A'C\)
\(\Delta A'AC\) vuông tại A nên theo Pitago ta có: \(A'{C^2} = A'{A^2} + A{C^2}\)
\(\Delta ABC\) vuông tại B nên theo Pitago ta có: \(A{C^2} = A{B^2} + B{C^2}\) \( = {b^2} + {c^2}\)
Do đó
\(\begin{array}{l}A'{C^2} = A'{A^2} + A{C^2}\\ = {a^2} + {b^2} + {c^2}\\ \Rightarrow A'C = \sqrt {{a^2} + {b^2} + {c^2}} \\ \Rightarrow R = \frac{{A'C}}{2} = \frac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}\end{array}\)
LG b
b) Tính bán kính của đường tròn là giao tuyến của mặt phẳng \((ABCD)\) với mặt cầu trên.
Phương pháp giải:
Đường tròn cần tìm là đường tròn ngoại tiếp hình chữ nhật \(ABCD\).
Lời giải chi tiết:
Giao tuyến của mặt phẳng\(\displaystyle ( ABCD)\) với mặt cầu ngoại tiếp hình hộp chữ nhật \(\displaystyle ABCD.A'B'C'D'\) là đường tròn ngoại tiếp hình chữ nhật \(\displaystyle ABCD\). Nên bán kính của đường trong giao tuyến là:
\(\displaystyle r = {1 \over 2}AC = {1 \over 2}\sqrt {{b^2} + {c^2}} \)
Loigiaihay.com













Danh sách bình luận