 Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
 Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Lý thuyết giá trị lớn nhất và nhỏ nhất của hàm số
Cho hàm số y = f(x) xác định trên tập D.
1. Định nghĩa
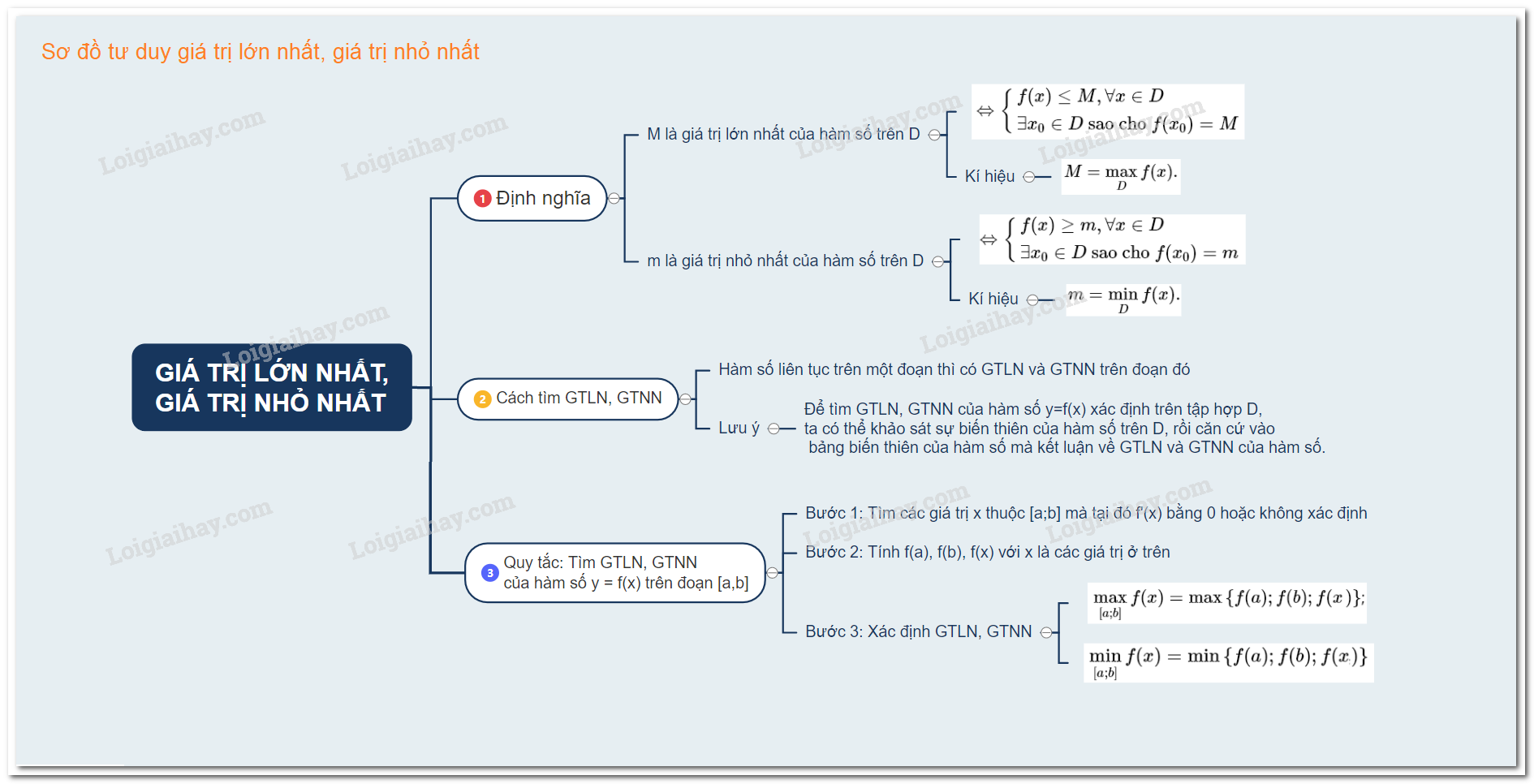
Cho hàm số \(y = f(x)\) xác định trên tập \(D.\)
- Số \(M\) là giá trị lớn nhất (GTLN) của hàm số \(f\) trên \(D \)
\(⇔\left\{ \matrix{
f(x) \le M,\forall x \in D \hfill \cr
\exists \, {x_0} \in D\text{ sao cho }f({x_0}) = M \hfill \cr} \right.\)
Kí hiệu : \(M=\underset{D}{\max} f(x).\)
- Số \(m\) là giá trị nhỏ nhất (GTNN) của hàm số \(f\) trên \(D\)
\(⇔\left\{ \matrix{
f(x) \ge m,\forall x \in D \hfill \cr
\exists \, {x_0} \in D\text{ sao cho }f({x_0}) = m \hfill \cr} \right.\)
Kí hiệu: \(m=\underset{D}{\min} f(x).\)
2. Cách tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
Định lí
Hàm số liên tục trên một đoạn thì có GTLN và GTNN trên đoạn đó.
Quy tắc tìm GTLN, GTNN của hàm số \(y = f(x)\) liên tục trên đoạn [a ; b]
- Tìm các điểm \(x_i ∈ (a ; b)(i = 1, 2, . . . , n)\) mà tại đó \(f'(x_i) = 0\) hoặc \(f'(x_i)\) không xác định.
- Tính \(f(a), f(b), f(x_i) (i = 1, 2, . . . , n) .\)
- Khi đó: \(\underset{[a;b]}{\max} f(x)=\max \left \{ f(a); f(b); f(x_{i}) \right \}\);
\(\underset{[a;b]}{\min} f(x)=\min \left \{ f(a); f(b); f(x_{i}) \right \}\)
3. Chú ý
Để tìm GTLN, GTNN của hàm số \(y=f(x)\) xác định trên tập hợp \(D\), ta có thể khảo sát sự biến thiên của hàm số trên \(D,\) rồi căn cứ vào bảng biến thiên của hàm số mà kết luận về GTLN và GTNN của hàm số.
Loigiaihay.com












Danh sách bình luận