Phần câu hỏi bài 10 trang 119, 120 Vở bài tập toán 9 tập 2

Câu 23

Diện tích hình vành khăn giữa hai đường tròn đồng tâm \((O ; R)\) và \((O ; r) (R > r)\) là \(12,5\pi \,c{m^2}\). Tiếp tuyến tại \(M\) của đường tròn \((O ; r)\) cắt đường tròn \((O ; R)\) tại \(A\) và \(B\). Độ dài dây cung \(AB\) của đường tròn lớn tiếp xúc với đường tròn nhỏ là:

(A) \(5:\sqrt 2 \)                       (B) \(5\)

(C) \(5\sqrt 2 \)                           (D) \(10\)

Khoanh tròn vào chữ cái trước kết quả đúng.

Phương pháp giải:

+ Sử dụng công thức tính diện tích hình tròn bán kính \(R\) là \(S = \pi {R^2}\), từ đó suy ra diện tích hình vành khăn

+ Sử dụng quan hệ giữa đường kính và dây cung, định lý Pytago để tính toán.

Lời giải chi tiết:

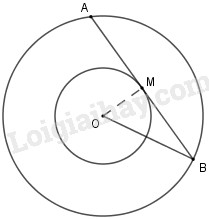
Diện tích hình tròn \(\left( {O;R} \right)\) là \({S_1} = \pi {R^2}\,\left( {c{m^2}} \right)\) , diện tích hình tròn \(\left( {O;r} \right)\) là \({S_2} = \pi {r^2}\,\left( {c{m^2}} \right)\)

Suy ra diện tích hình vành khăn là \(S = {S_1} - {S_2} = \pi {R^2} - \pi {r^2}\,\,\left( {c{m^2}} \right)\)

Từ bài cho ta có \(S = 12,5\pi \,\left( {c{m^2}} \right) \Rightarrow \pi {R^2} - \pi {r^2}\)\( = 12,5\pi  \Leftrightarrow {R^2} - {r^2} = 12,5\)

Xét đường tròn \(\left( {O;r} \right)\) có \(AB\) là tiếp tuyến tại \(M \Rightarrow OM \bot AB\)

Xét \(\left( {O;R} \right)\) có \(OM \bot AB\) nên \(M\) là trung điểm \(AB\) (quan hệ giữa dây và đường kính), suy ra \(AB = 2MB.\)

Xét tam giác \(OMB\) vuông tại \(M\), theo định lý Pytago ta có \(MB = \sqrt {O{B^2} - O{M^2}}  = \sqrt {{R^2} - {r^2}} \)  mà \({R^2} - {r^2} = 12,5\)(cmt) và \(AB = 2MB\) (cmt) nên \(AB = 2\sqrt {{R^2} - {r^2}}  = 2\sqrt {12,5}  \)\(= 5\sqrt 2 \,cm.\)

Chọn C.

Câu 24

Một hình vuông cạnh a và một đường tròn bán kính r có chu vi bằng nhau. Tỉ số giữa diện tích hình tròn và diện tích hình vuông là:

(A) \(4:\pi \)                       (B) \(\sqrt 2 :\pi \)

(C) \(\pi :\sqrt 2 \)                    (D) \(\pi :4\)

Khoanh tròn vào chữ cái trước kết quả đúng.

Phương pháp giải:

+ Hình vuông cạnh \(a\) có chu vi là \(4.a\) và diện tích là \({a^2}\)

+ Đường tròn bán kính \(r\) có chu vi \(C = 2\pi r\) và diện tích hình tròn là \(S = \pi {r^2}\)

Lời giải chi tiết:

Ta có:

Hình vuông cạnh \(a\) có chu vi là \(4.a\) và diện tích là \({a^2}\) và đường tròn bán kính \(r\) có chu vi \(C = 2\pi r\) và diện tích hình tròn là \(S = \pi {r^2}\) .

Vì theo giả thiết thì hình vuông và đường tròn có chu vi bằng nhau nên \(4a = 2\pi r \Rightarrow \dfrac{r}{a} = \dfrac{2}{\pi }\)

Tỉ số giữa diện tích hình tròn và diện tích hình vuông là \(\dfrac{{\pi {r^2}}}{{{a^2}}} = \pi {\left( {\dfrac{r}{a}} \right)^2} = \pi .\dfrac{4}{{{\pi ^2}}} = \dfrac{4}{\pi } = 4:\pi \) (vì \(\dfrac{r}{a} = \dfrac{2}{\pi }\) (cmt))

Chọn A. 

Loigiaihay.com