Bài 52 trang 122 Vở bài tập toán 9 tập 2

Giải bài 52 trang 122 VBT toán 9 tập 2. Hình vành khăn là phần hình tròn nằm giữa hai đường tròn đồng tâm (h.59).a) Tính diện tích của hình vành khăn theo R1 và R2 (Giả sử R1 > R2)...

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Đề bài

Hình vành khăn là phần hình tròn nằm giữa hai đường tròn đồng tâm (h.59).

a) Tính diện tích của hình vành khăn theo R₁ và R₂ (giả sử R₁ > R₂)

b) Tính diện tích của hình vành khăn khi R₁ = 10,5 cm, R₂ = 7,8 cm.

Phương pháp giải - Xem chi tiết

Sử dụng công thức tính diện tích hình tròn bán kính \(R\) là \(S = \pi {R^2}\) để suy ra diện tích hình vành khăn

Lời giải chi tiết

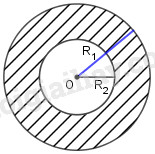
Gọi \(S\) là diện tích hình vành khăn;

\({S_1}\) là diện tích hình tròn \(\left( {O;{R_1}} \right)\);

\({S_2}\) là diện tích hình tròn \(\left( {O;{R_2}} \right)\);

Mà \({S_1} = \pi R_1^2\) và \({S_2} = \pi R_2^2;\)

\(S = {S_1} - {S_2}.\)

Vậy diện tích hình vành khăn là

\(S = \pi .10,{5^2} - \pi .7,{8^2} \)\(= \pi \left( {10,{5^2} - 7,{8^2}} \right) = 49,41\pi \,(cm^2)\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 5 phiếu

Bài tiếp theo

Bài 53 trang 122 Vở bài tập toán 9 tập 2
Giải bài 53 trang 122 VBT toán 9 tập 2. Lấy cạnh BC của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết cạnh BC = a...
Bài 51 trang 120 Vở bài tập toán 9 tập 2
Giải bài 51 trang 120 VBT toán 9 tập 2. a) Vẽ hình 58 (tạo bởi các cung tròn) với HI = 10 cm và HO = HI = 2cm. Nêu cách vẽ. b) Tính diện tích hình HOABINH (miễn gạch chéo)...
Bài 50 trang 120 Vở bài tập toán 9 tập 2
Giải bài 50 trang 120 VBT toán 9 tập 2. Diện tích hình tròn sẽ thay đổi như thế nào nếu:a) Bán kính tăng gấp đôi ?b) Bán kính tăng gấp ba ?c) Bán kính tăng k lần (k > 1) ?...
Bài 49 trang 120 Vở bài tập toán 9 tập 2
Giải bài 49 trang 120 VBT toán 9 tập 2. Tính diện tích một hình quạt tròn có bán kính 6 cm, số đo cung là 36 độ...
Bài 48 trang 120 Vở bài tập toán 9 tập 2
Giải bài 48 trang 120 VBT toán 9 tập 2. Chân một đống cát đổ trên một nền phẳng nằm ngang là một hình tròn có chu vi là 12 m. Hỏi chân đống cát đó chiếm một diện tích là bao nhiêu mét vuông ...
Phần câu hỏi bài 10 trang 119, 120 Vở bài tập toán 9 tập 2
Giải phần câu hỏi bài 10 trang 119, 120 VBT toán 9 tập 2. Diện tích hình vành khăn giữa hai đường tròn đồng tâm (O ; R) và (O ; r) (R > r) là 12,5pi xăng-ti-mét vuông. Tiếp tuyến tại M của đường tròn (O ; r) cắt đường tròn (O ; R) tại A và B...