-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI -CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Bài 2. Tỉ số lượng giác của góc nhọn
- Bài 3. Bảng lượng giác
- Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 5. Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời
- Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a khác 0) - PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số y = ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số y=ax^2 (a ≠ 0)
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Ôn tập chương 4 - Hàm số y=ax^2 (a khác 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp - Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, quạt tròn
- Ôn tập chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 46 trang 107 Vở bài tập toán 9 tập 1
Tổng hợp đề thi vào 10 tất cả các tỉnh thành trên toàn quốc
Toán - Văn - Anh
Đề bài
Cho hình 58. Tính khoảng cách AD (làm tròn đến chữ số thập phân thứ hai).
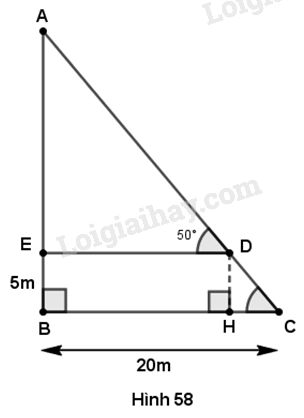
Phương pháp giải - Xem chi tiết
- Tìm độ dài cạnh huyền\(AC\) bằng cách lấy cạnh \(BC\) chia cho cos góc kề.
- Tìm độ dài cạnh huyền \(DC\) bằng cách lấy cạnh góc vuông \(DH\) chia cho \(\sin \) góc kề.
- Từ đó tìm độ dài cạnh \(AD.\)
Lời giải chi tiết
Trong tam giác vuông \(ABC,\) ta có :
\(\widehat C = \widehat {ADE} = {50^o}\) và \(AC = \dfrac{{BC}}{{\cos C}} = \dfrac{{20}}{{\cos {{50}^o}}} \approx 31,11\left( m \right).\)
Trong tam giác vuông \(DHC,\) ta có :
\(DH = EB = 5m\) và \(DC = \dfrac{{DH}}{{\sin C}} = \dfrac{5}{{\sin {{50}^o}}} \approx 6,53\left( m \right).\)
Vậy khoảng cách \(AD\) là:
\(AD = AC - DC \approx 31,11 - 6,53 \)\(= 24,58\left( m \right).\)
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 45 phút chương 1 phần Hình học 9 - Đề số 1
- Đề kiểm tra 45 phút chương 1 phần Hình học 9 - Đề số 2
- Bài 45 trang 107 Vở bài tập toán 9 tập 1
- Bài 44 trang 106 Vở bài tập toán 9 tập 1
- Bài 43 trang 106 Vở bài tập toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com. , cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
