Bài 45 trang 107 Vở bài tập toán 9 tập 1

Giải bài 45 trang 107 VBT toán 9 tập 1. Cho tam giác ABC có AB = 6m, AC = 4,5cm, BC = 7,5cm...

Đề bài

Cho tam giác ABC có AB = 6m, AC = 4,5cm, BC = 7,5cm

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH (làm tròn đến chữ số thập phân thứ hai).

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào ?

Phương pháp giải - Xem chi tiết

a) Áp dụng định lí Pi-ta-go đảo : Tam giác có tổng bình phương hai cạnh bằng bình phương cạnh kia thì tam giác đó là tam giác vuông để chứng minh.

Áp dụng tỉ số lượng giác \(\sin \alpha = \dfrac{\text{cạnh đối}}{\text{cạnh huyền}}\) để tìm độ lớn của góc \(B.\)

Tính độ lớn góc \(C\) bằng cách \(\widehat C = {90^o} - \widehat B.\)

Tính đường cao \(AH\) bằng cạnh huyền \(AB\) nhân với \(\sin \) góc đối.

b) Để \({S_{ABC}} = {S_{MBC}}\) thì cặp cạnh đáy và chiều cao tương ứng của hai tam giác bằng nhau.

Lời giải chi tiết

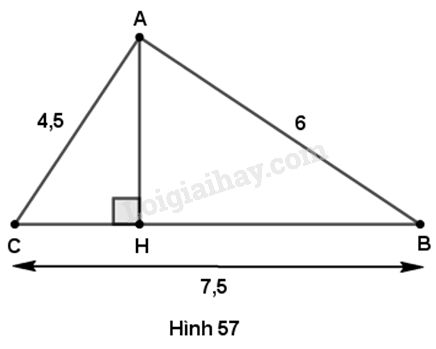
a) Tam giác \(ABC\) có :

\(A{B^2} + A{C^2} = {6^2} + 4,{5^2} \)\(= 7,{5^2} = B{C^2}.\)

Vậy tam giác \(ABC\) là tam giác vuông tại \(A.\)

Do đó, \(\sin B = \dfrac{{AC}}{{BC}} \)\(= 4,5:7,5 = 0,6\)

Suy ra \(\widehat B \approx {36^o}52'\) và \(\widehat C \approx {90^o} - {36^o}52' \)\(= {53^o}8'.\)

Trong tam giác vuông \(AHB\) có

\(AH = AB.\sin B = 6.0,6 = 3,6\left( {cm} \right).\)

b) \({S_{MBC}} = {S_{ABC}}\) khi đường cao kẻ từ \(M\) của tam giác \(MBC\) bằng \(AH.\) ( Do tam giác ABC và MBC có chung đáy BC). Từ đó suy ra \(M\) nằm trên hai đường thẳng song song với \(BC\) và cùng cách \(BC\) một khoảng \(3,6cm.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 6 phiếu

Bài tiếp theo

Bài 46 trang 107 Vở bài tập toán 9 tập 1
Giải bài 46 trang 107 VBT toán 9 tập 1. Cho hình 58. Tính khoảng cách AD (làm tròn đến chữ số thập phân thứ hai).
Đề kiểm tra 45 phút chương 1 phần Hình học 9 - Đề số 1
Giải đề kiểm tra 45 phút chương 1: Hệ thức lượng trong tam giác vuông đề số 1 trang 108 VBT toán lớp 9 tập 1 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài
Đề kiểm tra 45 phút chương 1 phần Hình học 9 - Đề số 2
Giải đề kiểm tra 45 phút chương 1: Hệ thức lượng trong tam giác vuông đề số 2 trang 109 VBT toán lớp 9 tập 1 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài
Bài 44 trang 106 Vở bài tập toán 9 tập 1
Giải bài 44 trang 106 VBT toán 9 tập 1. Từ một đỉnh ngọn đèn biển cao 38m so với mặt nước biển...
Bài 43 trang 106 Vở bài tập toán 9 tập 1
Giải bài 43 trang 106 VBT toán 9 tập 1. Tìm khoảng cách AB trong hình 55 (làm tròn đến mét)
Bài 42 trang 105 Vở bài tập toán 9 tập 1
Giải bài 42 trang 105 vbt toán 9 tập 1. Cho tam giác có một góc bằng 45o. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm...