Bài 3.9 trang 165 SBT giải tích 12
Giải bài 3.9 trang 165 sách bài tập giải tích 12. Tính các nguyên hàm sau đây:...
Tính các nguyên hàm sau đây:
LG câu a
a) \(\int {(x + \ln x){x^2}dx} \)
Phương pháp giải:
Tính nguyên hàm bằng công thức từng phần \(\int {udv} = uv - \int {vdu} \).
Giải chi tiết:
Đặt \(u = x + \ln x;dv = {x^2}dx\) \( \Rightarrow \left\{ \begin{array}{l}du = \left( {1 + \dfrac{1}{x}} \right)dx\\v = \dfrac{{{x^3}}}{3}\end{array} \right.\)
Khi đó \(\int {(x + \ln x){x^2}dx} \)\( = \dfrac{{{x^3}}}{3}\left( {x + \ln x} \right) - \int {\dfrac{{{x^3}}}{3}\left( {1 + \dfrac{1}{x}} \right)dx} \)
\( = \dfrac{{{x^4}}}{3} + \dfrac{{{x^3}}}{3}\ln x - \int {\left( {\dfrac{{{x^3}}}{3} + \dfrac{{{x^2}}}{3}} \right)dx} \) \( = \dfrac{{{x^4}}}{3} + \dfrac{{{x^3}}}{3}\ln x - \dfrac{{{x^4}}}{{12}} - \dfrac{{{x^3}}}{9} + C\) \( = \dfrac{{{x^4}}}{4} + \dfrac{{{x^3}}}{3}\left( {\ln x - \dfrac{1}{3}} \right) + C\).
LG câu b
b) \(\int {(x + {{\sin }^2}x)\sin xdx} \)
Phương pháp giải:
Tính nguyên hàm bằng công thức từng phần \(\int {udv} = uv - \int {vdu} \).
Giải chi tiết:
Đặt \(u = x + {\sin ^2}x,dv = \sin xdx\) \( \Rightarrow \left\{ \begin{array}{l}du = \left( {1 + 2\sin x\cos x} \right)dx\\v = - \cos x\end{array} \right.\)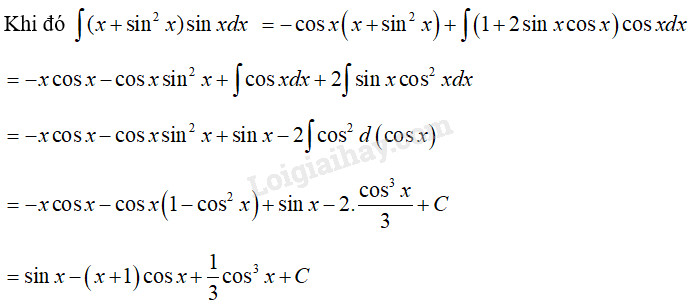
LG câu c
c) \(\int {(x + {e^x}){e^{2x}}dx} \)
Phương pháp giải:
Tính nguyên hàm bằng công thức từng phần \(\int {udv} = uv - \int {vdu} \).
Giải chi tiết:
Đặt \(u = x + {e^x},dv = {e^{2x}}dx\) \( \Rightarrow \left\{ \begin{array}{l}du = \left( {1 + {e^x}} \right)dx\\v = \dfrac{{{e^{2x}}}}{2}\end{array} \right.\)
LG câu d
d) \(\int {(x + \sin x)\dfrac{{dx}}{{{{\cos }^2}x}}} \)
Phương pháp giải:
Tính nguyên hàm bằng công thức từng phần \(\int {udv} = uv - \int {vdu} \).
Giải chi tiết:
Đặt \(\left\{ \begin{array}{l}u = x + \sin x\\dv = \dfrac{1}{{{{\cos }^2}x}}dx\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}du = \left( {1 + \cos x} \right)dx\\v = \tan x\end{array} \right.\)

Loigiaihay.com













Danh sách bình luận