-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 3.7 trang 164 SBT giải tích 12
Giải bài 3.7 trang 164 sách bài tập giải tích 12. Bằng cách biến đổi các hàm số lượng giác, hãy tính:...
Bằng cách biến đổi các hàm số lượng giác, hãy tính:
LG câu a
a) \(\int {{{\sin }^4}x} dx\)
Phương pháp giải:
Hạ bậc đưa về dạng tổng rồi tính nguyên hàm, sử dụng công thức nguyên hàm hàm số cơ bản \(\int {\cos kxdx} = \dfrac{{\sin kx}}{k} + C\).
Lời giải chi tiết:
Ta có: \({\sin ^4}x = \dfrac{{{{\left( {1 - \cos 2x} \right)}^2}}}{4}\)\( = \dfrac{1}{4}\left( {1 - 2\cos 2x + {{\cos }^2}2x} \right)\)
\( = \dfrac{1}{4}\left( {1 - 2\cos 2x + \dfrac{{1 + \cos 4x}}{2}} \right)\) \( = \dfrac{1}{4}\left( {\dfrac{3}{2} - 2\cos 2x + \dfrac{1}{2}\cos 4x} \right)\)
Khi đó \(\int {{{\sin }^4}x} dx\)\( = \int {\dfrac{1}{4}\left( {\dfrac{3}{2} - 2\cos 2x + \dfrac{1}{2}\cos 4x} \right)dx} \) \( = \int {\left( {\dfrac{3}{8} - \dfrac{1}{2}\cos 2x + \dfrac{1}{8}\cos 4x} \right)dx} \)
\( = \dfrac{3}{8}x - \dfrac{1}{2}.\dfrac{{\sin 2x}}{2} + \dfrac{1}{8}.\dfrac{{\sin 4x}}{4} + C\) \( = \dfrac{3}{8}x - \dfrac{{\sin 2x}}{4} + \dfrac{{\sin 4x}}{{32}} + C\)
LG câu b
b) \(\int {\dfrac{1}{{{{\sin }^3}x}}dx} \)
Phương pháp giải:
Nhân cả tử và mẫu của biểu thức dưới dấu nguyên hàm với \(\sin x\) rồi đổi biến \(t = \cos x\) để tìm nguyên hàm.
Lời giải chi tiết:
Ta có: \(\int {\dfrac{1}{{{{\sin }^3}x}}dx} \)\( = \int {\dfrac{{\sin x}}{{{{\sin }^4}x}}dx} \) \( = \int {\dfrac{{\sin x}}{{{{\left( {1 - {{\cos }^2}x} \right)}^2}}}dx} \)
Đặt \(t = \cos x \Rightarrow dt = - \sin xdx\) ta có:
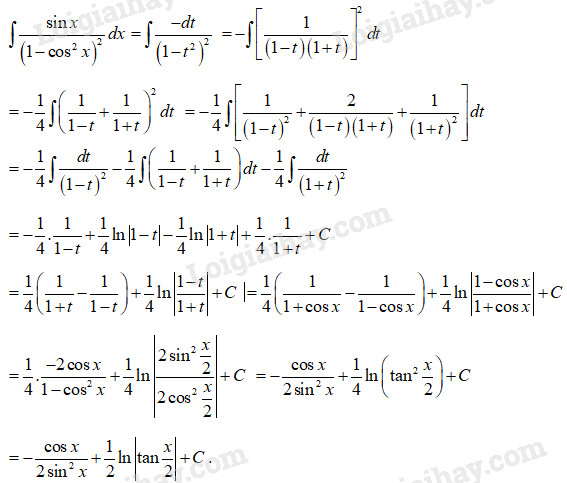
LG câu c
c) \(\int {{{\sin }^3}x{{\cos }^4}xdx} \)
Phương pháp giải:
Đổi biến \(u = \cos x\) tính nguyên hàm.
Lời giải chi tiết:
\(\int {{{\sin }^3}x{{\cos }^4}xdx} \)
Đặt \(t = \cos x \Rightarrow dt = - \sin xdx\).
Khi đó \(\int {{{\sin }^3}x{{\cos }^4}xdx} \)\( = \int {{{\sin }^2}x.{{\cos }^4}x.\sin xdx} \) \( = \int {\left( {1 - {t^2}} \right).{t^4}.\left( { - dt} \right)} \)
\( = \int {\left( { - {t^4} + {t^6}} \right)dt} \) \( = - \dfrac{{{t^5}}}{5} + \dfrac{{{t^7}}}{7} + C\) \( = - \dfrac{{{{\cos }^5}x}}{5} + \dfrac{{{{\cos }^7}x}}{7} + C\).
LG câu d
d) \(\int {{{\sin }^4}x{{\cos }^4}xdx} \)
Phương pháp giải:
Hạ bậc (sử dụng công thức nhân đôi) và tính nguyên hàm.
Lời giải chi tiết:
Ta có: \({\sin ^4}x{\cos ^4}x\)\( = {\left( {\dfrac{1}{2}\sin 2x} \right)^4} = \dfrac{1}{{{2^4}}}{\sin ^4}2x\) \( = \dfrac{1}{{16}}{\left( {{{\sin }^2}2x} \right)^2} = \dfrac{1}{{16}}.{\left[ {\dfrac{{1 - \cos 4x}}{2}} \right]^2}\)
\( = \dfrac{1}{{64}}{\left( {1 - \cos 4x} \right)^2}\) \( = \dfrac{1}{{64}}\left( {1 - 2\cos 4x + {{\cos }^2}4x} \right)\) \( = \dfrac{1}{{64}} - \dfrac{1}{{32}}\cos 4x + \dfrac{1}{{64}}.\dfrac{{1 + \cos 8x}}{2}\)
\( = \dfrac{3}{{128}} - \dfrac{1}{{32}}\cos 4x + \dfrac{1}{{128}}\cos 8x\)
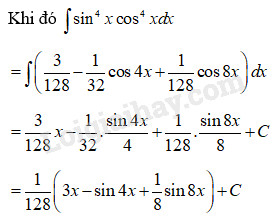
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3.8 trang 165 SBT giải tích 12
- Bài 3.9 trang 165 SBT giải tích 12
- Bài 3.10 trang 165 SBT giải tích 12
- Bài 3.11 trang 165 SBT giải tích 12
- Bài 3.12 trang 165 SBT giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
