Giải vở bài tập toán lớp 9 tập 1, tập 2 Bài 6. Cung chứa góc

Bài 31 trang 107 Vở bài tập toán 9 tập 2


Giải bài 31 trang 107 VBT toán 9 tập 2. Gọi cung chứa góc 55 độ ở bài 30 là cung AmB. Lấy điểm M1; M2 và cung AmB nằm cùng một phía đối với đường thẳng AB. Chứng minh rằng...

Đề bài

Gọi cung chứa góc \(55^\circ \) ở bài 30 là \(\overparen{AmB}\) . Lấy điểm \({M_1},{M_2}\) và cung \(AmB\) nằm cùng một phía đối với đường thẳng \(AB\). Chứng minh rằng :

a)  \(\widehat {A{M_1}B} > 55^\circ \) ;

b) \(\widehat {A{M_2}B} < 55^\circ\).

Phương pháp giải - Xem chi tiết

 Sử dụng:

+ Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn

+ Số đo của góc có đỉnh bên trong đường tròn bằng nửa hiệu số đo hai cung bị chắn

Lời giải chi tiết

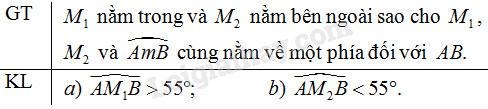
a)

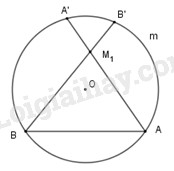
Gọi \(A'\),\(B'\) lần lượt là giao của \(A{M_1};B{M_1}\) với đường tròn.

Góc \(A{M_1}B\) là góc có đỉnh nằm trong đường tròn nên ta có :

\(\widehat {A{M_1}B}\)\( = \dfrac{1}{2}\) (sđ\(\overparen{AB}+\) sđ\( \overparen{A'B'}\)) 

Mà \(\widehat {AA'B} = \dfrac{1}{2}\) sđ\(\overparen{AB}\)\( = 55^\circ \) vì \(\dfrac{1}{2}\) (sđ\(\overparen{AB}+\) sđ\( \overparen{A'B'}\)) \( > \dfrac{1}{2}\)sđ \(\overparen{AB}\) nên \(\widehat {A{M_1}B} > 55^\circ \)

b)

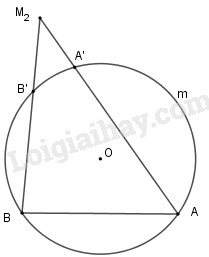
Góc \(A{M_2}B\) là góc có đỉnh nằm bên ngoài đường tròn nên ta có :

 \(\widehat {A{M_2}B} = \dfrac{1}{2}\) (sđ\(\overparen{AB}-\) sđ\( \overparen{A'B'}\)) 

Mà \(\widehat {AB'B} = \dfrac{1}{2}\) sđ\(\overparen{AB}\)\( = 55^\circ \) vì \(\dfrac{1}{2}\) (sđ\(\overparen{AB}-\) sđ\( \overparen{A'B'}\))\( < \dfrac{1}{2}\)sđ\(\overparen{AB}\) nên \(\widehat {A{M_2}B} < 55^\circ \) .

Loigiaihay.com


Bình chọn:
4.3 trên 4 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store