Bài 29 trang 105 Vở bài tập toán 9 tập 2

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\) có cạnh \(BC\) cố định. Gọi \(I\) là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm \(I\) khi \(A\) thay đổi.

Lời giải chi tiết

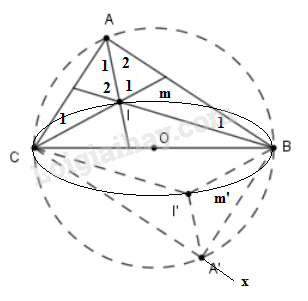
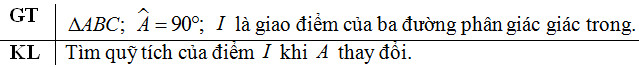
a) Phần thuận:

Điểm A luôn nhìn đoạn thẳng AB dưới một góc \(90^\circ \) nên quỹ tích điểm \(A\) là đường tròn đường kính \(BC.\)

Vì \(\widehat {BIC} = \widehat {{I_1}} + \widehat {{I_2}}\)                       (1)

\(\Delta AIB\) và \(\Delta AIC\) lần lượt có góc \({I_1}\) và \({I_2}\) là các góc ngoài, nên ta có :

\(\widehat {{I_1}} = \widehat {{B_1}} + \widehat {{A_1}}\)   (2) và \(\widehat {{I_2}} = \widehat {{A_2}} + \widehat {{C_1}}\)        (3)

Cộng (2) với (3) và từ (1), ta được \(\widehat {BIC} = \widehat {{A_1}} + \widehat {{B_1}} + \widehat {{A_2}} + \widehat {{C_1}}\)  mà \(\widehat {{B_1}} + \widehat {{C_1}}\)\( = \dfrac{{90^\circ }}{2}\) vì theo giả thiết \(AI;BI\) và \(CI\) là các đường phân giác của góc các góc \(A,B,C.\)

Do đó, \(\widehat {BIC} = \widehat A + 45^\circ  = 90^\circ  + 45^\circ  = 135^\circ\)\(  \Rightarrow \widehat {BIC}\) luôn không đổi.

Khi điểm \(A\) thay đổi trên đường tròn đường kính \(BC\) thì điểm I thay đổi và luôn nhìn đoạn thẳng BC dưới một góc \(135^\circ .\)

Vậy điểm I thuộc hai cung tròn chứa góc \(135^\circ \) và dựng cố định trên đoạn BC.

b) Phần đảo:

Lấy I’ bất kì trên cung \(Bm'C\) (hoặc cung \(BmC)\), ta chứng minh I’ là giao điểm của ba đường phân giác trong của tam giác \(A'BC\) vuông tại \(A'.\)

Nối \(BI';CI'\). Để xác định điểm \(A'\) ta dựng góc \(I'Bx\) bằng góc \(I'BC.\) Đường thẳng \(Bx\) cắt đường tròn đường kính \(BC\) chính là điểm \(A'.\) Nối \(A'\) với \(C\) và \(I'\) ta được tam giác \(A'BC\) vuông, \(\widehat {A'} = 90^\circ \) vì góc nội tiếp chắn nửa đường tròn

Vì \(I'\) nằm trên cung \(Bm'C\) nên \(\widehat {BI'C} = 135^\circ  \Rightarrow \widehat {I'BC} + \widehat {I'CB} = 45^\circ .\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 4 \right)\)

Mặt khác \(\widehat B + \widehat C = 90^\circ\)  (5) 

             \(\widehat B = \widehat {I'BC}\)\( + \widehat {I'BA'}\)

             \(\widehat C = \widehat {I'CB}\)\( + \widehat {I'OA'}\) nên từ (5) ta có :

\(\widehat {I'BA'} + \widehat {I'BC} + \widehat {I'CB} + \widehat {I'CA'} = 90^\circ .\)

Từ (4) \( \Rightarrow \widehat {I'BA'} + \widehat {I'CA'} = 45^\circ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 6 \right)\)

Từ (4) và (6) ta có \(\widehat {I'BC} + \widehat {I'CB} = \widehat {I'BA'} + \widehat {I'CA'}.\)

Mà \(\widehat {I'BA'} = \widehat {I'BC}\) theo cách dựng,  nên ta có  \(\widehat {I'CB} = \widehat {I'CA'} \Rightarrow I'C\) là đường phân giác  của góc \(C\), hay \(I'\) là  giao điểm các đường phân giác trong của tam giác \(A'BC.\)

c) Kết luận: Quỹ tích các điểm I là giao điểm của ba đường phân giác trong thỏa mãn \(\widehat {BIC} = 135^\circ \) là điểm thuộc hai cung tròn chứa góc \(135^\circ \) dựng trên đoạn BC.

Loigiaihay.com