Bài 26 trang 74 Vở bài tập toán 9 tập 1

Đề bài

a) Vẽ đồ thị của các hàm số \(y = x + 1;\,\,y = \dfrac{1}{{\sqrt 3 }} + \sqrt 3 ;\,y = \sqrt 3 x - \sqrt 3 \)

b) Gọi \(\alpha ,\,\,\beta ,\,\,\gamma \) lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox. Chứng minh rằng \(\tan \alpha  = 1,\,\tan \beta  = \dfrac{1}{{\sqrt 3 }},\,\,\tan \gamma  = \sqrt 3 \) . Tính số đo các góc \(\alpha ,\,\,\beta ,\,\,\gamma \)

Lời giải chi tiết

a) Đồ thị hàm số \(y = x + 1\)

- Cho \(x = 0\) thì \(y = 1\)

- Cho \(y = 0\) thì \(x =  - 1\)

Vẽ đường thẳng đi qua điểm \(A\left( {0;1} \right);B\left( { - 1;0} \right)\) thì ta được đồ thị của hàm số \(y = x + 1\).

Đồ thị hàm số \(y = \dfrac{1}{{\sqrt 3 }}x + \sqrt 3 \) :

- Cho \(x = 0\) thì \(y = \sqrt 3 \)

- Cho \(y = 0\) thì \(x =  - 3\)

Vẽ đường thẳng đi qua hai điểm \(C\left( {0;\sqrt 3 } \right);D\left( { - 3;0} \right)\) thì được đồ thị của hàm số \(y = \dfrac{1}{{\sqrt 3 }}x + \sqrt 3 \)

Đồ thị hàm số \(y = \sqrt 3 x - \sqrt 3 \) :

- Cho \(x = 0\) thì \(y =  - \sqrt 3 \)

- Cho \(y = 0\) thì \(x = 1\)

Vẽ đường thẳng đi qua hai điểm \(E\left( {0; - \sqrt 3 } \right);F\left( {1;0} \right)\) thì được đồ thị của hàm số \(y = \sqrt 3 x - \sqrt 3 \).

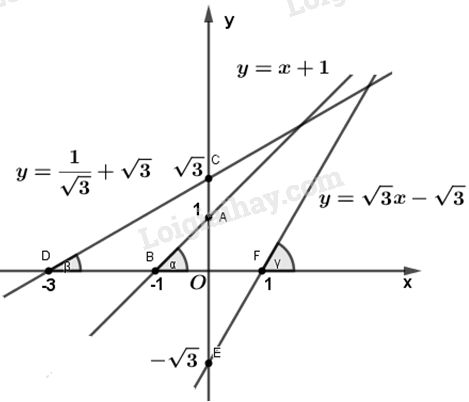
b) Tam giác vuông OAB có \(\tan \alpha  = \dfrac{{OA}}{{OB}} = 1\).

    Tam giác vuông OCD có \(\tan \beta  = \dfrac{{OC}}{{OD}} = \dfrac{{\sqrt 3 }}{3} \)\(= \dfrac{1}{{\sqrt 3 }}\)

Ta có: \(\tan \gamma  = \tan \widehat {OFE}\) (đối đỉnh)

Tam giác vuông OFE có : \(\tan \widehat F = \dfrac{{OE}}{{OF}}\)\( = \sqrt 3 \)

Vậy \(\tan \alpha  = 1,\tan \beta  = \dfrac{1}{{\sqrt 3 }},\tan \gamma  \)\(= \sqrt 3 \)

Dùng máy tính bỏ túi tính ta được

\(\alpha  = {45^o},\beta  = {30^o},\gamma  = {60^o}\).

Loigiaihay.com