Giải bài 3 trang 68 SGK Hình học 12

Tính tọa độ các đỉnh của hình hộp.

Đề bài

Cho hình hộp \(ABCD.A'B'C'D'\) biết \(A = (1; 0; 1), B = (2; 1; 2), D = (1; -1; 1)\), \(C' (4; 5; -5)\). Tính tọa độ các đỉnh còn lại của hình hộp.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng các vector bằng nhau.

Hai vector \(\overrightarrow u \left( {{x_1};{y_1};{z_1}} \right) = \overrightarrow v \left( {{x_2};{y_2};{z_2}} \right) \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\)

Lời giải chi tiết

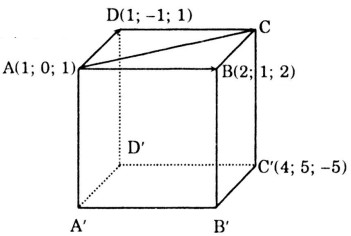
Ta có:

\(\eqalign{
& \overrightarrow {AB} = \left( {1;1;1} \right) \cr
& \overrightarrow {A{\rm{D}}} = \left( {0; - 1;0} \right) \cr
& \overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \Leftrightarrow \left\{ \matrix{
{x_C} - 2 = 0 \hfill \cr
{y_C} - 1 = - 1 \hfill \cr
{z_C} - 2 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_C} = 2 \hfill \cr
{y_C} = 0 \hfill \cr
{z_C} = 2 \hfill \cr} \right. \cr} \)

Vậy \(C = (2; 0; 2)\)

Suy ra \(\overrightarrow {CC'} = \left( {2;5; - 7} \right)\)

Từ \(\overrightarrow {AA'} = \overrightarrow {BB'} = \overrightarrow {DD'} = \overrightarrow {CC'} = \left( {2;5; - 7} \right)\)

Suy ra \(\left\{ \matrix{
{x_{A'}} - 1 = 2 \hfill \cr
{y_{A'}} - 0 = 5 \hfill \cr
{z_{A'}} - 1 = - 7 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_{A'}} = 3 \hfill \cr
{y_{A'}} = 5 \hfill \cr
{z_{A'}} = - 6 \hfill \cr} \right.\)

Vậy \(A’ (3; 5; -6)\)

Tương tự

\(\begin{array}{l}\left\{ \begin{array}{l}{x_{B'}} - 2 = 2\\{y_{B'}} - 1 = 5\\{z_{B'}} - 2 = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} = 4\\{y_{B'}} = 6\\{z_{B'}} = - 5\end{array} \right. \Rightarrow B'\left( {4;6; - 5} \right)\\\left\{ \begin{array}{l}{x_{D'}} - 1 = 2\\{y_{D'}} + 1 = 5\\{z_{D'}} - 1 = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{D'}} = 3\\{y_{D'}} = 4\\{z_{D'}} = - 6\end{array} \right. \Rightarrow D'\left( {3;4; - 6} \right)\end{array}\)

loigiaihay.com