Bài 94 trang 140 Sách bài tập Hình học lớp 12 Nâng cao

LG a

Tính cos của góc giữa hai đường thẳng AP và BC’.

Lời giải chi tiết:

Ta chọn hệ toạ độ Oxyz có gốc là đỉnh A, tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA' (h.105).

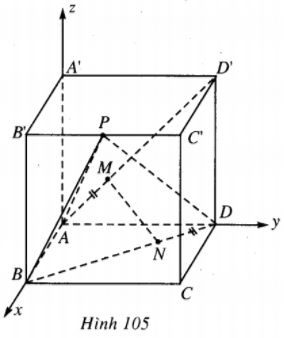
Khi đó :

         \(\eqalign{  & A = \left( {0;0;0} \right)  \cr  & B = \left( {a;0;0} \right)  \cr  & D = \left( {0;a;0} \right)  \cr  & C = \left( {a;a;0} \right) \cr} \)  \(\eqalign{  & A' = \left( {0;0;a} \right)  \cr  & B' = \left( {a;0;a} \right)  \cr  & D' = \left( {0;a;a} \right)  \cr  & C' = \left( {a;a;a} \right) \cr} \)

          \(P = \left( {a;{a \over 2};a} \right)\)

Ta có \(\overrightarrow {AP}  = \left( {a;{a \over 2};a} \right)\)

                       \(\overrightarrow {BC'}  = \left( {0;a;a} \right).\)

Gọi \(\alpha \) là góc giữa hai đường thẳng \(AP\) và \(BC'\) ta có :

         \(\cos \alpha  = {{\left| {0 + {{{a^2}} \over 2} + {a^2}} \right|} \over {\sqrt {{a^2} + {{{a^2}} \over 2} + {a^2}} .\sqrt {{a^2} + {a^2}} }} = {1 \over {\sqrt 2 }} \Rightarrow \alpha  = {45^o}\)

LG b

Tính thể tích khối tứ diện APBC’.

Lời giải chi tiết:

Ta có : \(\overrightarrow {AP}  = \left( {a;{a \over 2};a} \right)\), \(\overrightarrow {AB}  = {\rm{ }}\left( {a;0;0} \right),\overrightarrow {AC'}  = (a;a;a)\)

\(\eqalign{  &  \Rightarrow \left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right] = \left( {\left| {\matrix{   {{a \over 2}} & a  \cr   0 & 0  \cr  } } \right|;\left| {\matrix{   a & a  \cr   0 & a  \cr  } } \right|;\left| {\matrix{   a & {{a \over 2}}  \cr   a & 0  \cr  } } \right|} \right) \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \left( {0;{a^2}; - {{{a^2}} \over 2}} \right)  \cr  &  \Rightarrow \left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right].\overrightarrow {AC'}  = 0 + {a^3} - {{{a^3}} \over 2} = {{{a^3}} \over 2}. \cr} \)

Vậy \({V_{APBC'}} = {1 \over 6}\left| {\left[ {\overrightarrow {AP} ,\overrightarrow {AB} } \right].\overrightarrow {AC'} } \right| = {1 \over 6}.{{{a^3}} \over 2} = {{{a^3}} \over {12}}.\) 

LG c

Chứng minh MN luôn song song với mặt phẳng (A’D’CB) khi k thay đổi.

Lời giải chi tiết:

Mặt phẳng \(\left( {A'D'CB} \right)\) song song với trục Oy nên có phương trình :

       \(px{\rm{ }} + {\rm{ }}qz{\rm{ }} + {\rm{ }}n{\rm{ }} = 0\) \(\left( {n \ne 0,{p^2} + {q^2} > 0} \right).\)

Vì mặt phẳng này đi qua \(A',B,C\) nên ta xác định được p = q và n = -pa.

Cho p = 1, ta được phương trình mp\(\left( {A'D'CB} \right)\) là \(x + z - {\rm{ }}a = {\rm{ }}0\). Vectơ pháp tuyến của mặt phẳng này là \(\overrightarrow n  = {\rm{ }}\left( {1{\rm{ }};{\rm{ }}0{\rm{ }};{\rm{ }}1} \right).\)

Từ giả thiết \(M \in AD',{\rm{ }}N \in DB;{\rm{ }}AM = {\rm{ }}DN = k\), ta tính được :

                      \(M = \left( {0;{k \over {\sqrt 2 }};{k \over {\sqrt 2 }}} \right),N = \left( {{k \over {\sqrt 2 }};{{a\sqrt {2 } -k} \over {\sqrt 2 }};0} \right).\)

Suy ra \(\overrightarrow {MN}  = \left( {{k \over {\sqrt 2 }};{{a\sqrt {2 } -2k} \over {\sqrt 2 }}; - {k \over {\sqrt 2 }}} \right).\)

Ta có \(\overrightarrow {MN} .\overrightarrow n  = 1.{k \over {\sqrt 2 }} + 0\left( {{{a\sqrt {2 }-2 k} \over {\sqrt 2 }}} \right) + 1.\left( { - {k \over {\sqrt 2 }}} \right) = 0\)

\(\Rightarrow \overrightarrow {MN}  \bot \overrightarrow n .\)

Rõ ràng \(N \notin mp\left( {A'D'CB} \right).\) Suy ra MN song song với mp\(\left( {A'D'CB} \right).\)

LG d

Tìm k để đoạn MN ngắn nhất.

Lời giải chi tiết:

Ta có \(M{N^2} = {\left( {{k \over {\sqrt 2 }}} \right)^2} + {\left( {{{a\sqrt {2 }-2 k} \over {\sqrt 2 }}} \right)^2} + {\left( { - {k \over {\sqrt 2 }}} \right)^2}.\)

\(\eqalign{  &  = 3{k^2} - 2a\sqrt 2 k + {a^2}  \cr  &  = 3\left[ {{{\left( {k - {{a\sqrt 2 } \over 3}} \right)}^2} + {{{a^2}} \over 9}} \right] \ge 3{{{a^2}} \over 9} = {{{a^2}} \over 3}. \cr} \)

\(M{N^2}\) nhỏ nhất bằng \({{{a^2}} \over 3}\) khi \(k = {{a\sqrt 2 } \over 3}\) (thoả mãn điều kiện \(0{\rm{ }} < k{\rm{ }} < {\rm{ }}a\sqrt 2 \) ).

Vậy MN ngắn nhất bằng \({{a\sqrt 3 } \over 3}\) khi \(k = {{a\sqrt 2 } \over 3}\).

LG e

Khi đoạn MN ngắn nhất, chứng minh rằng MN là đường vuông góc chung của AD’ và DB, đồng thời MN song song với A’C.

Lời giải chi tiết:

Khi MN ngắn nhất thì \(k = {{a\sqrt 2 } \over 3}\) Khi đó \(\overrightarrow {MN}  = \left( {{a \over 3};{a \over 3};{{ - a} \over 3}} \right).\)

Ta lại có \(\overrightarrow {AD'}  = {\rm{ }}\left( {0;a;{\rm{ }}a} \right),\overrightarrow {DB} {\rm{ }} = (a; - a;0)\) nên \(\overrightarrow {MN} .\overrightarrow {AD'}  = {\rm{ }}0,\overrightarrow {MN} .\overrightarrow {DB}  = {\rm{ }}0.\)

Vậy MN là đường vuông góc chung của AD' và DB.

Mặt khác \(\overrightarrow {A'C}  = \left( a;a; - a\right) = 3\overrightarrow {MN} \), chứng tỏ \(\overrightarrow {MN} \), \(\overrightarrow {A'C} \) cùng phương. Do \(N \not\in A'C\)  nên \(MN//A'C.\)

Loigiaihay.com