 Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
 Bài 1. Sự đồng biến, nghịch biến của hàm số
Bài 1. Sự đồng biến, nghịch biến của hàm số
Tính đơn điệu của hàm số
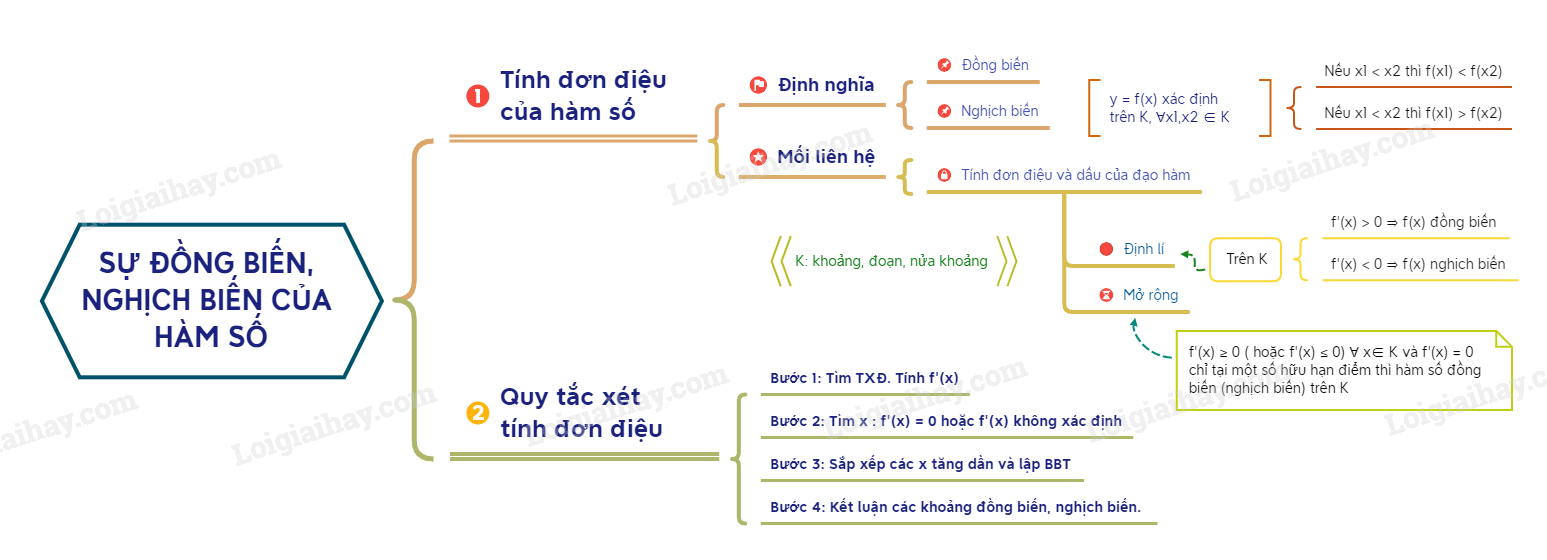
Tính đơn điệu của hàm số, khảo sát sự biến thiên, tính đơn điệu của hàm số, điều kiện để hàm số đồng biến - nghịch biến
1. Định nghĩa
Hàm số \(f\) xác định trên \(K\). Với mọi \(x_1, x_2\) thuộc \(K\) mà \( x_1 > x_2\)
+) nếu \(f(x_1)>f(x_2)\) thì \(f\) tăng trên \(K\)
+) nếu \(f(x_1)<f(x_2)\) thì \(f\) giảm trên \(K\).
Chú ý:
- Hàm số tăng hoặc giảm trên \(K\) được gọi chung là hàm số đơn điệu trên \(K\).
- \(K\) có thể là một khoảng, một đoạn hoặc một nửa khoảng.
2. Điểu kiện cần đế hàm số đơn điệu
Cho hàm số \(f\) có đạo hàm trên khoảng \(K\)
- Nếu \(f\) tăng trên \(K\) thì \(f'(x)>0\), với mọi \(x\) thuộc \(K\).
- Nếu \(f\) giảm trên \(K\) thì \(f'(x)< 0\), với mọi \(x\) thuộc \(K\).
3. Điều kiện đủ để hàm số đơn điệu
Cho hàm sổ \(f\) có đạo hàm trên khoảng \(K\)
- Nếu \(f'(x) > 0\) với mọi \(x\) thuộc \(K\) thì \(f\) tăng trên \(K\).
- Nếu \(f'(x) < 0\) với mọi \(x\) thuộc \(K\) thì \(f\) giảim trên \(K\).
Chú ý: Nếu \(f'(x) ≥ 0\) \(\forall x \in K\) (hoặc \(f’(x) \le 0\), \(\forall x \in K\)) và \(f’(x) = 0\) chỉ tại một số hữu hạn điểm thuộc \(K\) thì hàm số \(f\) tăng (hoặc giảm) trên \(K\).
Loigiaihay.com












Danh sách bình luận