 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Bài 1. Sự đồng biến, nghịch biến của hàm số
Bài 1. Sự đồng biến, nghịch biến của hàm số
Trả lời câu hỏi 1 trang 4 SGK Giải tích 12
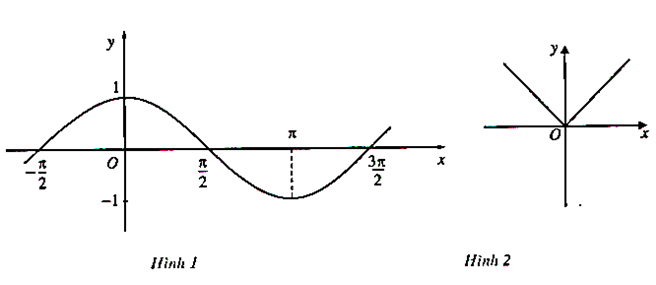
Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số (y = cos x) trên đoạn (displaystyle left[ {{{ - pi } over 2};,{{3pi } over 2}} right]) và các hàm số (displaystyle y = left| x right|) trên khoảng (displaystyle left( { - infty ; + infty } right)).
Đề bài
Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số \(y = \cos x\) trên đoạn \(\displaystyle \left[ {{{ - \pi } \over 2};\,{{3\pi } \over 2}} \right]\) và các hàm số \(\displaystyle y = \left| x \right|\) trên khoảng \(\displaystyle \left( { - \infty ; + \infty } \right)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Trên khoảng K: đồ thị hàm số đi lên (từ trái sang phải) thì hàm số đồng biến trên K.
- Trên khoảng K: đồ thị hàm số đi xuống (từ trái sang phải) thì hàm số nghịch biến trên K.
Lời giải chi tiết
- Hàm số \(y = \cos x\) trên đoạn \(\displaystyle \left[ {{{ - \pi } \over 2};\,{{3\pi } \over 2}} \right]\)
Các khoảng tăng: \(\displaystyle \left( {{{ - \pi } \over 2};\,0} \right);\,\left( {\pi ;\,{{3\pi } \over 2}} \right)\)
Các khoảng giảm: \(\displaystyle \left( {0;\pi } \right)\).
- Hàm số \(\displaystyle y = \left| x \right|\) trên khoảng \(\displaystyle \left( { - \infty ; + \infty } \right)\)
Khoảng tăng: \(\displaystyle \left( {0, + \infty } \right)\)
Khoảng giảm \(\displaystyle \left( { - \infty ,0} \right)\)
Loigiaihay.com












Danh sách bình luận