 Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
 Bài 5. Phương trình mũ và phương trình lôgarit
Bài 5. Phương trình mũ và phương trình lôgarit
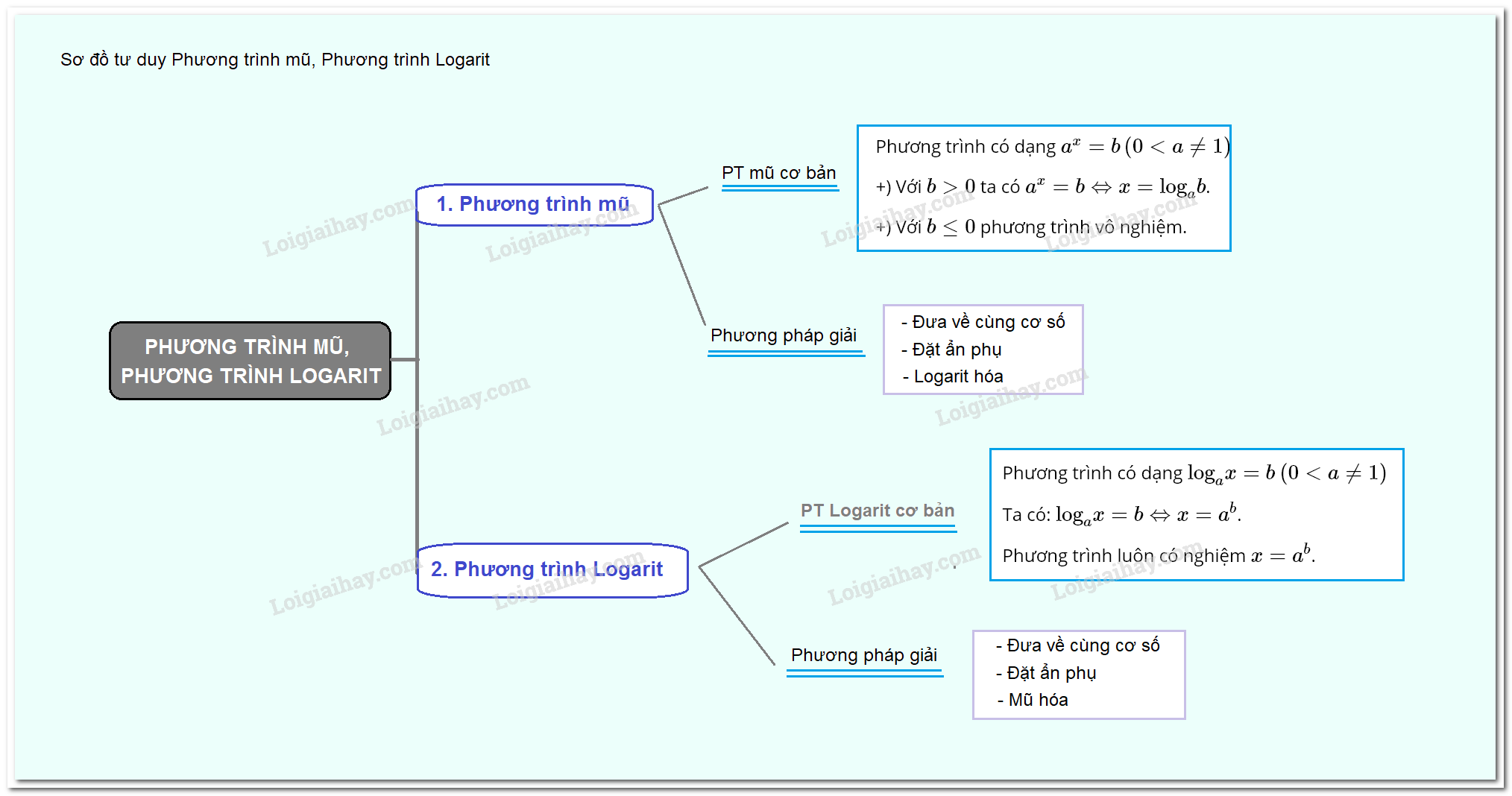
Lý thuyết phương trình mũ và phương trình lôgarit
1. Phương trình mũ cơ bản và phương trình lôgarit cơ bản
I. PHƯƠNG TRÌNH MŨ
1. Phương trình mũ cơ bản
Phương trình có dạng \({a^x} = b\left( {0 < a \ne 1} \right)\)
+) Với \(b > 0\) ta có \({a^x} = b \Leftrightarrow x = {\log _a}b\).
+) Với \(b \le 0\) phương trình vô nghiệm.
Ví dụ: Giải phương trình \({5^x} = 125\).
Ta có:
\(\begin{array}{l}{5^x} = 125\\ \Leftrightarrow x = {\log _5}125\\ \Leftrightarrow x = 3\end{array}\)
2. Cách giải một số phương trình mũ đơn giản
a) Đưa về cùng cơ số
Ví dụ: Giải phương trình \({\left( {\frac{1}{2}} \right)^{2x - 1}} = {2^{3x}}\)
Ta có:
\(\begin{array}{l}{\left( {\frac{1}{2}} \right)^{2x - 1}} = {2^{3x}}\\ \Leftrightarrow {2^{ - 2x + 1}} = {2^{3x}}\\ \Leftrightarrow - 2x + 1 = 3x\\ \Leftrightarrow 1 = 5x\\ \Leftrightarrow x = \dfrac{1}{5}\end{array}\)
b) Đặt ẩn phụ
Ví dụ: Giải phương trình \({4^x} - {2^{x + 1}} + 1 = 0\).
Ta có:
\(\begin{array}{l}{4^x} - {2^{x + 1}} + 1 = 0\\ \Leftrightarrow {\left( {{2^x}} \right)^2} - {2.2^x} + 1 = 0\end{array}\)
Đặt \(t = {2^x} > 0\) ta được:
\(\begin{array}{l}{t^2} - 2t + 1 = 0\\ \Leftrightarrow {\left( {t - 1} \right)^2} = 0\\ \Leftrightarrow t - 1 = 0\\ \Leftrightarrow t = 1\end{array}\)
\(\begin{array}{l} \Rightarrow {2^x} = 1\\ \Leftrightarrow x = {\log _2}1\\ \Leftrightarrow x = 0\end{array}\)
c) Logarit hóa
Ví dụ: Giải phương trình \({3^x}{.2^{{x^2}}} = 1\).
Logarit hai vế cơ số \(3\) ta được:
\(\begin{array}{l}{\log _3}\left( {{3^x}{{.2}^{{x^2}}}} \right) = {\log _3}1\\ \Leftrightarrow {\log _3}{3^x} + {\log _3}{2^{{x^2}}} = 0\\ \Leftrightarrow x + {x^2}{\log _3}2 = 0\\ \Leftrightarrow x\left( {1 + x{{\log }_3}2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\1 + x{\log _3}2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - \dfrac{1}{{{{\log }_3}2}} = - {\log_2}3\end{array} \right.\end{array}\)
d) Đưa về phương trình tích.
Phương pháp:
- Bước 1: Tìm điều kiện xác định (nếu có)
- Bước 2: Biến đổi phương trình về dạng tích \(AB = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
- Bước 3: Giải các phương trình \(A = 0,B = 0\) tìm nghiệm.
- Bước 4: Kiểm tra điều kiện và kết luận nghiệm.
e) Sử dụng bất đẳng thức, tính đơn điệu của hàm số.
Phương pháp:
- Bước 1: Tìm điều kiện xác định.
- Bước 2: Có thể làm một trong hai cách sau:
Cách 1: Biến đổi phương trình sao cho một vế là hàm số đơn điệu, một vế là hằng số hoặc một vế là hàm đồng biến và vế còn lại là hàm số nghịch biến.
Cách 2: Biến đổi phương trình về dạng \(f\left( u \right) = f\left( v \right)\) với \(f\) là hàm số đơn điệu.
- Bước 3: Nhẩm một nghiệm của phương trình trên.
- Bước 4: Kết luận nghiệm duy nhất của phương trình.
II. PHƯƠNG TRÌNH LOGARIT
1. Phương trình logarit cơ bản
Phương trình có dạng \({\log _a}x = b\) \(\left( {0 < a \ne 1} \right)\)
Ta có: \({\log _a}x = b \Leftrightarrow x = {a^b}\).
Phương trình luôn có nghiệm \(x = {a^b}\).
Ví dụ: Giải phương trình \({\log _5}x = - 2\).
Ta có: \({\log _5}x = - 2 \Leftrightarrow x = {5^{ - 2}} \Leftrightarrow x = \dfrac{1}{{25}}\).
2. Cách giải một số phương trình logarit
a) Đưa về cùng cơ số
Ví dụ: Giải phương trình \({\log _2}x + {\log _4}x = 1\)
Ta có:
\(\begin{array}{l}{\log _2}x + {\log _4}x = 1\\ \Leftrightarrow {\log _2}x + \dfrac{1}{2}{\log _2}x = 1\\ \Leftrightarrow \dfrac{3}{2}{\log _2}x = 1\\ \Leftrightarrow {\log _2}x = \dfrac{2}{3}\\ \Leftrightarrow x = {2^{\frac{2}{3}}}\\ \Leftrightarrow x = \sqrt[3]{4}\end{array}\)
b) Đặt ẩn phụ
Ví dụ: Giải phương trình \(\dfrac{1}{{\ln x}} + \dfrac{1}{{\ln x - 1}} = \dfrac{5}{6}\).
ĐK: \(\left\{ \begin{array}{l}x > 0\\\ln x \ne 0\\\ln x \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x \ne 1\\x \ne e\end{array} \right.\)
Đặt \(t = \ln x\left( {t \ne 0,t \ne 1} \right)\) ta được:
\(\begin{array}{l}\dfrac{1}{t} + \dfrac{1}{{t - 1}} = \dfrac{5}{6}\\ \Leftrightarrow \dfrac{{6t - 6 + 6t}}{{6t\left( {t - 1} \right)}} = \dfrac{{5t\left( {t - 1} \right)}}{{6t\left( {t - 1} \right)}}\\ \Rightarrow 12t - 6 = 5{t^2} - 5t\\ \Leftrightarrow 5{t^2} - 17t + 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = \dfrac{2}{5}\end{array} \right.\left( {TM} \right)\\ \Rightarrow \left[ \begin{array}{l}\ln x = 3\\\ln x = \dfrac{2}{5}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = {e^3}\\x = {e^{\frac{2}{5}}}\end{array} \right.\left( {TM} \right)\end{array}\)
Vậy phương trình có tập nghiệm \(S = \left\{ {{e^3};{e^{\frac{2}{5}}}} \right\}\).
c) Mũ hóa
Ví dụ: Giải phương trình \({\log _3}\left( {3 - {3^x}} \right) = 1 + x\)
ĐK: \(3 - {3^x} > 0 \Leftrightarrow {3^x} < 3 \Leftrightarrow x < 1\)
Ta có:
\(\begin{array}{l}{\log _3}\left( {3 - {3^x}} \right) = 1 + x\\ \Leftrightarrow 3 - {3^x} = {3^{1 + x}}\\ \Leftrightarrow 3 - {3^x} = {3.3^x}\\ \Leftrightarrow 3 = {4.3^x}\\ \Leftrightarrow {3^x} = \dfrac{3}{4}\\ \Leftrightarrow x = {\log _3}\dfrac{3}{4}\\ \Leftrightarrow x = 1 - {\log _3}4\left( {TM} \right)\end{array}\)
d) Đưa về phương trình tích.
Phương pháp:
- Bước 1: Tìm điều kiện xác định (nếu có)
- Bước 2: Biến đổi phương trình về dạng tích \(AB = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
- Bước 3: Giải các phương trình \(A = 0,B = 0\) tìm nghiệm.
- Bước 4: Kiểm tra điều kiện và kết luận nghiệm.
e) Sử dụng bất đẳng thức, tính đơn điệu của hàm số.
Phương pháp:
- Bước 1: Tìm điều kiện xác định.
- Bước 2: Có thể làm một trong hai cách sau:
Cách 1: Biến đổi phương trình sao cho một vế là hàm số đơn điệu, một vế là hằng số hoặc một vế là hàm đồng biến và vế còn lại là hàm số nghịch biến.
Cách 2: Biến đổi phương trình về dạng \(f\left( u \right) = f\left( v \right)\) với \(f\) là hàm số đơn điệu.
- Bước 3: Nhẩm một nghiệm của phương trình trên.
- Bước 4: Kết luận nghiệm duy nhất của phương trình.
Loigiaihay.com












Danh sách bình luận