Bài 2. Hàm số bậc nhất

Bài 8 trang 56 Vở bài tập toán 9 tập 1

Giải bài 8 trang 56 VBT toán 9 tập 1. Hãy biểu diễn các điểm sau trên mặt phẳng tọa độ: A(-3 ; 0), B(-1 ; 1), C(0 ; 3), D(1 ; 1), E(3 ; 0), F(1 ; -1), G(0 ; -3), H(-1 ; -1).

Đề bài

Hãy biểu diễn các điểm sau trên mặt phẳng tọa độ: \(A(-3 ; 0), B(-1 ; 1), C(0 ; 3), D(1 ; 1),\)\( E(3 ; 0), F(1 ; -1), G(0 ; -3), H(-1 ; -1).\)

Phương pháp giải - Xem chi tiết

Biểu diễn điểm \(M\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ ta làm như sau :

- Vẽ đường thẳng song song với trục tung Oy tại hoành độ \(x = {x_0}\).

- Vẽ đường thẳng song song với trục hoành Ox tại tung độ \(y = {y_0}\).

- Giao điểm của hai đường thẳng trên chính là điểm \(M\left( {{x_0};{y_0}} \right)\).

Ghi nhớ : Những điểm trên trục hoành có tung độ \({y_0} = 0\) và những điểm trên trục tung có hoành độ \({x_0} = 0\).

Lời giải chi tiết

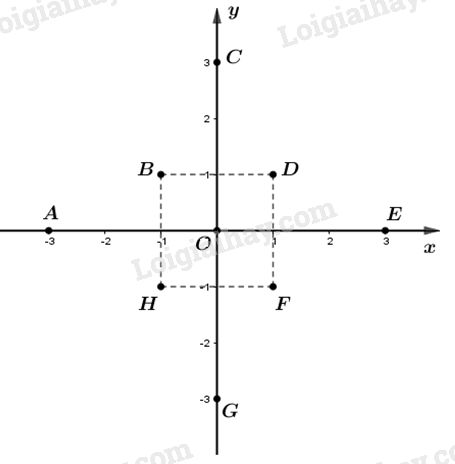
+) Điểm \(A(-3; 0) \Rightarrow\) hoành độ là \(-3\) và tung độ là \(0\)

\(\Rightarrow \) điểm \(A\) nằm trên trục hoành, tại vị trí điểm \(-3\).

+) Điểm \(B(-1; 1) \Rightarrow\) hoành độ là \(-1\) và tung độ là \(1\)

+) Điểm \(C(0; 3) \Rightarrow\) hoành độ là \(0\) và tung độ là \(3\)

\(\Rightarrow \) điểm \(C\) nằm trên trục tung, tại vị trí điểm \(3\).

+) Điểm \(D(1; 1) \Rightarrow\) hoành độ là \(1\) và tung độ là \(1\)

+) Điểm \(E(3; 0) \Rightarrow\) hoành độ là \(3\) và tung độ là \(0\)

\(\Rightarrow \) điểm \(E\) nằm trên trục hoành, tại vị trí điểm \(3\).

+) Điểm \(F(1; -1) \Rightarrow\) hoành độ là \(1\) và tung độ là \(-1\)

+) Điểm \(G(0; -3) \Rightarrow\) hoành độ là \(0\) và tung độ là \(-3\)

\(\Rightarrow \) điểm \(C\) nằm trên trục tung, tại vị trí điểm \(-3\).

+) Điểm \(H(-1; -1) \Rightarrow\) hoành độ là \(-1\) và tung độ là \(-1\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4 trên 6 phiếu

Bài 9 trang 57 Vở bài tập toán 9 tập 1
Giải bài 9 trang 57 VBT toán 9 tập 1. Với những giá trị nào của m thì mỗi hàm số sau là hàm số bậc nhất ?
Bài 10 trang 57 Vở bài tập toán 9 tập 1
Giải bài 10 trang 57 VBT toán 9 tập 1. Cho hàm số bậc nhất ...
Bài 7 trang 56 Vở bài tập toán 9 tập 1
Giải bài 7 trang 56 VBT toán 9 tập 1. Một hình chữ nhật có các kích thước là 20cm và 30cm...
Bài 6 trang 55 Vở bài tập toán 9 tập 1
Giải bài 6 trang 55 VBT toán 9 tập 1. Cho hàm số bậc nhất y = (m – 2)x + 3. Tìm các giá trị của m để hàm số...
Phần câu hỏi bài 2 trang 55 Vở bài tập toán 9 tập 1
Giải phần câu hỏi bài 2 trang 55 VBT toán 9 tập 1. Trong các hàm số dưới đây, hàm số không phải là hàm số bậc nhất là...