Bài 40 trang 115 Vở bài tập toán 9 tập 2

Đề bài

Trên đường tròn bán kính \(R\) lần lượt đặt theo cùng một chiều, kể từ điểm \(A\), ba cung \(AB, BC, CD\) sao cho sđ\(\overparen{AB}= {60^o}\), sđ\(\overparen{BC}= {90^o}\), sđ\(\overparen{CD}= {120^o}\).

a) Tứ giác \(ABCD\) là hình gì ?

d) Chứng minh rằng hai đường chéo của tứ giác \(ABCD\) vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác \(ABCD\) theo \(R\).

Lời giải chi tiết

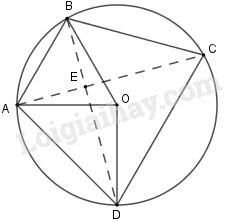
a) Xét cung \(DA\) , ta có : 

sđ\(\overparen{DA}=\) \(360^\circ  - \) (sđ \(\overparen{AB}+\) sđ\(\overparen{BC}+\) sđ\(\overparen{CD}\)) \( = 360^\circ  - 270^\circ  = 90^\circ .\)

Vậy sđ\(\overparen{DA}= 90^\circ \) ta có : sđ\(\overparen{BC}\) = sđ\(\overparen{DA}\)

 \( \Rightarrow \widehat {ACD} = \widehat {BAC} = \dfrac{1}{2}\) sđ\(\overparen{AD}\). Do đó, ta có \(AB//DC\) và \(\overparen{BC}= \overparen{AD}\) \( \Rightarrow BC = DA.\)

Vậy tứ giác\(ABCD\) là hình thang cân.

b) Gọi \(E\) là giao điểm của hai đường chéo \(AC\) và \(BD\). Góc  \(AEB\) có đỉnh  nằm bên trong đường tròn nên ta có:

\(\widehat {AEB} = \dfrac{1}{2}\) (sđ \(\overparen{AB}\) + sđ \(\overparen{CD}\)). Từ giả thiết ta có sđ\(\overparen{CD}\)\( = 120^\circ ;\) sđ\(\overparen{AB}\) \( = 60^\circ \)

Vậy  \(\widehat {AEB} = 90^\circ  \Rightarrow AC \bot BD.\)

c) Ta có \(\widehat {AOB} = \) sđ\(\overparen{AB}\) \( = 60^\circ \) là góc ở tâm và  \(OA = OB = AB\)

\( \Rightarrow \Delta {\rm A}OB\) là tam giác đều.

Vậy  \(AB = R.\)

Ta có \(\widehat {AOD} = \) sđ \(\overparen{AD}\) \( = 90^\circ \)và \(OA = OD = R \Rightarrow \Delta AOD\) là tam giác vuông cân.

\(A{D^2} = O{A^2} + O{D^2} = 2{R^2}.\) Vậy \(AD = R\sqrt 2 \) và \(BC = AD = R\sqrt 2 ,\) vì \(ABCD\) là hình thang cân.

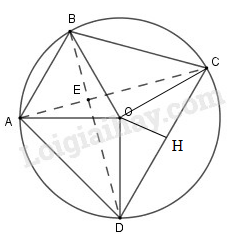
Kẻ \(OH \bot CD\) tại \(H\) 

Vì sđ\(\overparen{CD}\) \( = 120^\circ \) \(\Rightarrow \widehat{COD}=120^0.\)

Lại có \(\Delta DOC\) cân tại \(O\) có \(OH\) là đường cao nên \(OH\) cũng là đường phân giác

\( \Rightarrow \widehat{HOC}=\widehat{DOC}:2=120^0:2=60^0.\)

Xét \(\Delta OCH\) vuông tại \(H\) ta có:

\(HC=OC.\sin \widehat{COH}=\dfrac{R\sqrt{3}}{2}.\)

Mà \(H\) là trung điểm của \(CD\) (định lý đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy).

\(\Rightarrow CD=2.CH=R\sqrt3.\)

Vậy \(AB = R;DC = R\sqrt3;BC = AD = R\sqrt 2 \) 

Loigiaihay.com