Bài 39 trang 114 Vở bài tập toán 9 tập 2
Giải bài 39 trang 114 VBT toán 9 tập 2. a) Vẽ tam giác đều ABC cạnh a = 3cm b) Vẽ tiếp đường tròn (O ; R) ngoại tiếp tam giác đều ABC. Tính R c) Vẽ tiếp đường tròn (O ; r) nội tiếp tam giác đều ABC. Tính r ...
Đề bài
a) Vẽ tam giác đều \(ABC\) cạnh \(a = 3cm\)
b) Vẽ tiếp đường tròn \((O ; R)\) ngoại tiếp tam giác đều \(ABC\). Tính \(R\)
c) Vẽ tiếp đường tròn \((O ; r)\) nội tiếp tam giác đều \(ABC\). Tính \(r\)
d) Vẽ tiếp tam giác đều \(IJK\) ngoại tiếp đường tròn \((O ; R)\).
Phương pháp giải - Xem chi tiết
Sử dụng: Tâm tam giác đều vừa là tâm đường tròn ngoại tiếp và vừa là tâm đường tròn nội tiếp.
Tính bán kính dựa vào định lý Pytago và tính chất trọng tâm tam giác.
Lời giải chi tiết
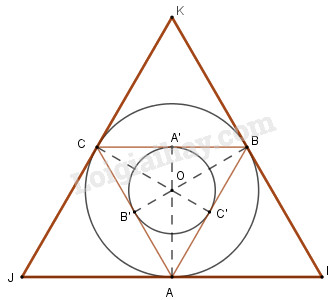
a) Vẽ tam giác đều \(ABC\), cạnh \(a = 3cm\) bằng thước và compa.
b) Vẽ đường tròn \(\left( {O;R} \right)\) ngoại tiếp \(\Delta ABC\) :
- Gọi \(O\) là giao điểm của ba đường trung trực \(AA',BB',CC'\) của tam giác đều\(ABC\) nên \(O\) là tâm của đường tròn ngoại tiếp \(\Delta ABC.\)
- Vẽ đường tròn tâm \(\left( {O;R} \right)\) tâm \(O\) bán kính \(R = OA\), ta được đường tròn ngoại tiếp tam giác đều \(ABC\) vì nó đi qua ba đỉnh của tam giác đều \(ABC.\)
Ta có \(AA'\) là đường cao của tam giác đều \(ABC\) cạnh \(a\) ,
\( \Rightarrow AA' = \dfrac{{a\sqrt 3 }}{2};R = OA = \dfrac{2}{3}A\,A'\)\( = \dfrac{a}{{\sqrt 3 }}.\)
Vậy bán kính của đường tròn ngoại tiếp \(R = \dfrac{a}{{\sqrt 3 }}.\)
c) Vẽ đường tròn \(\left( {O;r} \right)\) nội tiếp:
Tại tâm \(O\) vẽ bán kính \(r = OA'\) . Ta được đường tròn nội tiếp tam giác \(ABC\) vì \(\left( {O;r} \right)\) tiếp xúc với \(AB;BC;AC\) theo thứ tự tại \(C',A',B'.\)
Mà \(OA' = \dfrac{1}{3}.AA' = \dfrac{a}{{2\sqrt 3 }}cm\)
Vậy \(r = \dfrac{a}{{2\sqrt 3 }}.\)
d) Vẽ tiếp tam giác đều \(I\,JK\) ngoại tiếp đường tròn \(\left( {O;R} \right)\) :
Vẽ ba tiếp tuyến với đường tròn \(\left( {O;R} \right)\) tại \(A,B,C\). Giao điểm của chúng là \(I;J;K.\)Ta được tam giác đều \(IJK\)ngoại tiếp đường tròn \(\left( {O;R} \right)\). \(IJK\) là tam giác đều có các góc bằng \(60^\circ .\)
Loigiaihay.com













Danh sách bình luận