Bài 34 trang 110 Vở bài tập toán 9 tập 2
Giải bài 34 trang 110 VBT toán 9 tập 2. Cho ABCD là tứ giác nội tiếp đường tròn tâm M, biết góc DAB bằng 80 độ, góc DAM bằng 30 độ, góc BMC bằng 70 độ ...
Đề bài
Cho \(ABCD\) là tứ giác nội tiếp đường tròn tâm \(M\), biết \(\widehat {DAB} = {80^0},\)\(\widehat {DAM} = {30^0},\)\(\widehat {BMC} = {70^0}\). Hãy tính số đo góc \(MAB;\)\( BCM;\)\( AMB ; DMC ; AMD ; MCD\) và \(BCD\).
Phương pháp giải - Xem chi tiết
+ Sử dụng các định lý: “Trong tứ giác nội tiếp, tổng hai góc đối bằng \(180^\circ \)”; “Tổng ba góc trong tam giác bằng \(180^\circ \)”.
+ Sử dụng tính chất tam giác cân
Lời giải chi tiết
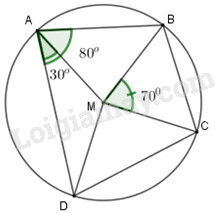
Nối tâm \(M\) của đường tròn với các đỉnh \(A,B,C,D.\)
Vì \(ABCD\) nội tiếp đường tròn ta có :
\(\widehat {DAB} + \widehat {BCD} = 180^\circ \)\( \Leftrightarrow \widehat {BCD} = 180^\circ - 80^\circ = 100^\circ ;\)
\(\widehat {MAB} = \widehat {DAB} - \widehat {DAM}\)\( = 80^\circ - 30^\circ = 50^\circ .\)
+ Xét \(\Delta BMC\) cân vì \(MB = MC\)
Ta có \(\widehat {MBC} = \widehat {BCM}\)
\( \Rightarrow 2\widehat {BCM} = 180^\circ - \widehat {BMC}\)\( = 180^\circ - 70^\circ = 110^\circ .\) Vậy \(\widehat {BCM} = 55^\circ .\)
+ Xét \(\Delta BMA\) cân vì \(MB = MA.\)
Ta có \(\widehat {MAB} = \widehat {ABM}\)\( \Rightarrow \widehat {AMB} = 180^\circ - 2.\widehat {MAB}\)\( = 180^\circ - 2.50^\circ = 80^\circ \) .
Vậy \(\widehat {AMB} = 80^\circ .\)
+ Xét \(\Delta DMA\) cân vì \(MD = MA.\)
Ta có \(\widehat {MAD} = \widehat {ADM}\)\( \Rightarrow \widehat {AMD} = 180^\circ - 2.\widehat {ADM} \)\(= 180^\circ - 60^\circ = 120^\circ .\)
Vậy \(\widehat {AMD} = 120^\circ .\)
Từ các kết quả trên ta có
\(\widehat {DMC} = 360^\circ - \left( {\widehat {AMD} + \widehat {AMB} + \widehat {BMC}} \right) \)\(= 360^\circ - \left( {120^\circ + 80^\circ + 70^\circ } \right) = 90^\circ \)
Vậy \(\widehat {DMC} = 90^\circ \)
Xét \(\Delta DMC\) cân vì \(MD = MC.\) Ta có \(\widehat {MCD} = \widehat {CDM}\)
\( \Rightarrow 2\widehat {MCD} = 180^\circ - \widehat {DMC} \)\(= 180^\circ - 90^\circ = 90^\circ \).
Vậy \(\widehat {MCD} = 45^\circ ,\widehat {BCD} = 100^\circ .\)
Loigiaihay.com













Danh sách bình luận