-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 3.32 trang 178 SBT giải tích 12
Giải bài 3.32 trang 178 sách bài tập giải tích 12. Tính thể tích vật thể:...
Tính thể tích vật thể:
LG a
a) Có đáy là một tam giác cho bởi: \(\displaystyle y = x,y = 0\), và \(\displaystyle x = 1\). Mỗi thiết diện vuông góc với trục \(\displaystyle Ox\) là một hình vuông.
Phương pháp giải:
Sử dụng công thức tính thể tích \(\displaystyle V = \int\limits_a^b {S\left( x \right)dx} \)
Lời giải chi tiết:
Dựng hình:
Với \(\displaystyle \forall x \in \left[ {0;1} \right]\), thiết diện là hình vuông cạnh \(\displaystyle x\), diện tích thiết diện \(\displaystyle S\left( x \right) = {x^2}\).
Vậy \(\displaystyle V = \int\limits_0^1 {S(x)dx = \int\limits_0^1 {{x^2}dx = \left. {\dfrac{{{x^3}}}{3}} \right|_0^1= \dfrac{1}{3}} } \)
LG b
b) Có đáy là một hình tròn giới hạn bởi \(\displaystyle {x^2} + {y^2} = 1\). Mỗi thiết diện vuông góc với trục \(\displaystyle Ox\) là một hình vuông.
Phương pháp giải:
Sử dụng công thức tính thể tích \(\displaystyle V = \int\limits_a^b {S\left( x \right)dx} \)
Lời giải chi tiết:
Dựng hình:
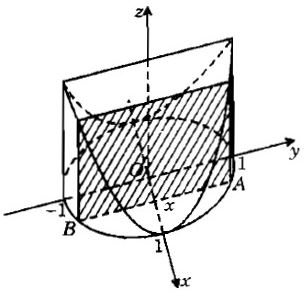
Thiết diện vuông góc trục \(\displaystyle Ox\) tại \(\displaystyle x \in {\rm{[}} - 1;1]\) là hình vuông cạnh \(\displaystyle AB\) , trong đó \(\displaystyle A\left( {x;y} \right)\) với \(\displaystyle y = \sqrt {1 - {x^2}} \).
Khi đó, \(\displaystyle AB = 2\sqrt {1 - {x^2}} \). Diện tích thiết diện là: \(\displaystyle S(x) = 4(1 - {x^2})\) .
Vậy \(V = \int\limits_{ - 1}^1 {4\left( {1 - {x^2}} \right)dx} \) \(= 4\left. {\left( {x - \dfrac{{{x^3}}}{3}} \right)} \right|_{ - 1}^1 \) \(= 4\left( {\dfrac{2}{3} + \dfrac{2}{3}} \right) = \dfrac{{16}}{3}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3.33 trang 178 SBT giải tích 12
- Bài 3.34 trang 178 SBT giải tích 12
- Bài 3.35 trang 178 SBT giải tích 12
- Bài 3.36 trang 179 SBT giải tích 12
- Bài 3.37 trang 179 SBT giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
