Bài 24 trang 148 Vở bài tập toán 9 tập 2

Giải bài 24 trang 148 VBT toán 9 tập 2. Hãy tính thể tích các hình dưới đây theo các kích thước đã cho (h.85) (đơn vị: cm)...

Đề bài

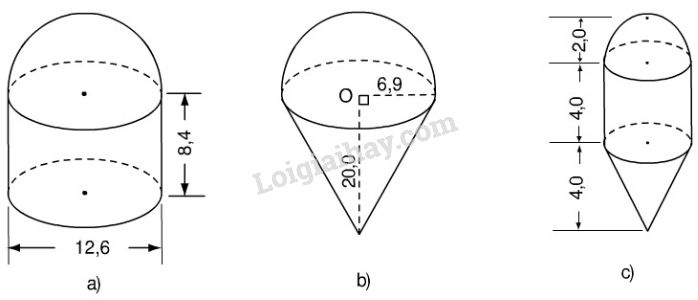
Hãy tính thể tích các hình dưới đây theo các kích thước đã cho (h.85) (đơn vị: cm)

Phương pháp giải - Xem chi tiết

Thể tích hình nón có bán kính đáy \(r\) và chiều cao \(h\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

Thể tích hình trụ có bán kính đáy \(r\) và chiều cao \(h\) là \(V = \pi {r^2}h\).

Thể tích hình cầu có bán kính đáy \(r\) là \(V = \dfrac{4}{3}\pi {r^3}\).

Lời giải chi tiết

Từ kích thước trên hình 85. c), ta có bán kính đáy \(R\) của các hình trụ, hình nón đều bằng bán kính nửa hình cầu và bằng \(2.\) Và \({h_T} = 4cm\); \({h_n} = 4cm.\)

Do đó, \(V = \dfrac{1}{2}{V_c} + {V_T} + {V_n};\)

\({V_c} = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {2^3}=\dfrac{32}{3}\pi \)

\({V_T} = \pi {R^2}h = \pi {2^2}.4 =16\pi \)

\({V_n} = \dfrac{1}{3}\pi {R^2}h=\dfrac{1}{3}\pi .{2^2}2 = \dfrac{16}{3}\pi\)

Vậy \(V = \dfrac{1}{2}{V_c} + {V_T} + {V_n}\) \( = \dfrac{2}{3}\pi \cdot 2^3 + \pi \cdot 16 + \dfrac{1}{3}\pi \cdot 16 \)\(= \pi \left( {\dfrac{{16}}{3} + 16 + \dfrac{{16}}{3}} \right) = \dfrac{{80}}{3}\pi \left( {c{m^3}} \right)\)

Trả lời : Thể tích của hình 85. c) là \(V = \dfrac{{80}}{3}\pi \left( {c{m^3}} \right).\)

Phần a) và phần b) ta có thể tính như sau:

a) Thể tích hình cần tính gồm một hình trụ có bán kính đáy \(R=12,6:2=6,3,\) chiều cao \(h=8,4\) và nửa hình cầu có bán kính \(R=12,6:2=6,3.\)

Thể tích hình trụ: \(V_1=\pi R^2 h=\pi.6,3^2.8,4=333,4 \pi \, cm^3.\)

Thể tích nửa hình cầu: \(V_2=\dfrac{1}{2}.\dfrac{4}{3}\pi R^3\)\(=\dfrac{2}{3}.\pi .6,3^3=166,7\pi \, cm^3.\)

\(\Rightarrow V=V_1+V_2\)\(=333,4 \pi +166,7\pi= 500,1 \pi \, cm^3.\)

b) Thể tích hình cần tính gồm một hình nón có bán kính đáy \(R=6,9,\) chiều cao \(h=20\) và nửa hình cầu có bán kính \(R=6,9.\)

Thể tích hình nón: \(V_1=\dfrac{1}{3}.\pi R^2 h\)\(=\dfrac{1}{3}.\pi.6,9^2.20=317,4 \pi \, cm^3.\)

Thể tích nửa hình cầu: \(V_2=\dfrac{1}{2}.\dfrac{4}{3}\pi R^3\)\(=\dfrac{2}{3}.\pi .6,9^3=219\pi \, cm^3.\)

\(\Rightarrow V=V_1+V_2\)\(=317,4 \pi +219\pi= 536,4 \pi \, cm^3.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Đề kiểm tra 45 phút chương 4 phần Hình học 9 - Đề số 1
Giải đề kiểm tra 45 phút chương 4: Hình trụ - Hình nón - Hình cầu Đề số 1 trang 148 VBT toán lớp 9 tập 2 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài
Đề kiểm tra 45 phút chương 4 phần Hình học 9 - Đề số 2
Giải đề kiểm tra 45 phút chương 4: Hình trụ - Hình nón - Hình cầu Đề số 2 trang 149 VBT toán lớp 9 tập 2 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài
Bài 23 trang 146 Vở bài tập toán 9 tập 2
Giải bài 23 trang 146 VBT toán 9 tập 2. Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA=a, OB=b (a, b cùng đơn vị: cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB...
Bài 22 trang 146 Vở bài tập toán 9 tập 2
Giải bài 22 trang 146 VBT toán 9 tập 2. Hãy tính diện tích toàn phần của các hình tương ứng theo các kích thước đã cho trên hình 83...
Bài 21 trang 145 Vở bài tập toán 9 tập 2
Giải bài 21 trang 145 VBT toán 9 tập 2. Hãy tính thể tích, diện tích bề mặt (xung quanh) của một chi tiết máy kích thước đã cho trên hình 82...