Bài 22 trang 146 Vở bài tập toán 9 tập 2

Giải bài 22 trang 146 VBT toán 9 tập 2. Hãy tính diện tích toàn phần của các hình tương ứng theo các kích thước đã cho trên hình 83...

Đề bài

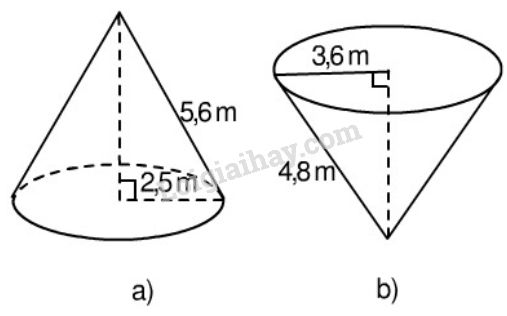
Hãy tính diện tích toàn phần của các hình tương ứng theo các kích thước đã cho trên hình 83.

Phương pháp giải - Xem chi tiết

Hình nón có bán kính đáy \(r\), chiều cao \(h\) và đường sinh \(l\) thì có

Diện tích xung quanh hình nón \({S_{xq}} = \pi rl\)

Diện tích toàn phần hình nón \({S_{tp}} = \pi rl + \pi {r^2}\)

Lời giải chi tiết

Theo kích thước trên hình 83, ta có :

Hình 83 a) \({r_1} = 2,5m\); \({l_1} = 5,6m\).

Hình 83 b) \({r_2} = 3,6m\); \({l_2} = 4,8m\).

+ Tính diện tích toàn phần ở hình a) : \({S_{tp}} = {S_d} + {S_{xq}}.\)

Từ công thức tính diện tích hình tròn và diện tích xung quanh của hình nón ta có :

\({S_d} = \pi r_1^2 = 6,25\pi \left( {{m^2}} \right);\) \({S_1} = \pi {r_1}{l_1} = 14\pi \left( {{m^2}} \right).\)

Vậy diện tích toàn phấn của hình nón là \({S_{tp}} = 6,25\pi + 14\pi = 20,25\pi \left( {{m^2}} \right).\)

+) Tương tự trên, tính cho trường hợp b)

\({S_{tp}} = {\rm{ }}{S_{xq}} + {\rm{ }}{S_{đáy}} = {\rm{ }}\pi {\rm{ }}.{\rm{ }}3,6{\rm{ }}.{\rm{ }}4,8{\rm{ }} + {\rm{ }}\pi {\rm{ }}.{\rm{ }}3,{6^2} \)

\( = {\rm{ }}30,24\pi{\rm{ }}({m^2})\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 23 trang 146 Vở bài tập toán 9 tập 2
Giải bài 23 trang 146 VBT toán 9 tập 2. Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA=a, OB=b (a, b cùng đơn vị: cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB...
Bài 24 trang 148 Vở bài tập toán 9 tập 2
Giải bài 24 trang 148 VBT toán 9 tập 2. Hãy tính thể tích các hình dưới đây theo các kích thước đã cho (h.85) (đơn vị: cm)...
Đề kiểm tra 45 phút chương 4 phần Hình học 9 - Đề số 1
Giải đề kiểm tra 45 phút chương 4: Hình trụ - Hình nón - Hình cầu Đề số 1 trang 148 VBT toán lớp 9 tập 2 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài
Đề kiểm tra 45 phút chương 4 phần Hình học 9 - Đề số 2
Giải đề kiểm tra 45 phút chương 4: Hình trụ - Hình nón - Hình cầu Đề số 2 trang 149 VBT toán lớp 9 tập 2 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài
Bài 21 trang 145 Vở bài tập toán 9 tập 2
Giải bài 21 trang 145 VBT toán 9 tập 2. Hãy tính thể tích, diện tích bề mặt (xung quanh) của một chi tiết máy kích thước đã cho trên hình 82...