 Giải SBT toán hình học và giải tích 12 cơ bản
Giải SBT toán hình học và giải tích 12 cơ bản
 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài 1.35 trang 21 SBT giải tích 12
Giải bài 1.35 trang 21 sách bài tập giải tích 12. Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
LG a
\(y = \dfrac{x}{{4 + {x^2}}}\) trên khoảng \(( - \infty ; + \infty )\)
Phương pháp giải:
- Tính đạo hàm và tìm nghiệm.
- Lập bảng biến thiên và kết luận.
Giải chi tiết:
Ta có: \(y' = \dfrac{{4 - {x^2}}}{{{{(4 + {x^2})}^2}}};\)\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
Bảng biến thiên:
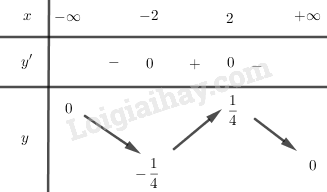
Từ đó ta có \(\mathop {\min }\limits_R f(x) = - \dfrac{1}{4};\mathop {\max }\limits_R f(x) = \dfrac{1}{4}\)
LG b
\(y = \dfrac{1}{{\cos x}}\) trên khoảng \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\)
Phương pháp giải:
- Tính đạo hàm và tìm nghiệm.
- Lập bảng biến thiên và kết luận.
Giải chi tiết:
Ta có: \(y' = \dfrac{{\sin x}}{{{{\cos }^2}x}};\)\(y' = 0 \Rightarrow x = \pi \in \left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\)
Bảng biến thiên:
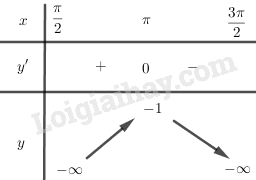
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: \(\mathop {\max }\limits_{\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)} y = y(\pi ) = - 1\)
Loigiaihay.com












Danh sách bình luận