-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 10 trang 170 SBT hình học 12
Giải bài 10 trang 170 sách bài tập hình học 12. Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0)...
Đề bài
Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0)
a) Viết phương trình của mặt phẳng (P) qua A và vuông góc với SB;
b) Tìm tọa độ của các điểm B' là gia của (P) với đường thẳng SB, C' là giao của (P) với đường thẳng SC;
c) Tính thể tích tứ diện SAB'C';
d) Tìm điểm đối xứng với B qua mặt phẳng (P);
e) Chứng minh các điểm A, B, C, B', C' cùng thuộc một mặt cầu. Viết phương trình của mặt cầu đó và phương trình của mặt phẳng tiếp xúc với mặt cầu đó tại C'.
Lời giải chi tiết
a) \(\overrightarrow {SB} = \left( {1;2; - 2} \right)\)
Phương trình (P) đi qua A và nhận \(\overrightarrow {SB} \) làm VTPT là:
x + 2y - 2z = 0.
b) Phương trình đường thẳng SB: \(\left\{ \begin{array}{l}x = t\\y = 2t\\z = 2 - 2t\end{array} \right.\).
Để tìm B' ta giải hệ \(\left\{ \begin{array}{l}x + 2y - 2z = 0\\x = t\\y = 2t\\z = 2 - 2t\end{array} \right.\)
\( \Rightarrow t + 2.2t - 2\left( {2 - 2t} \right) = 0\) \( \Leftrightarrow 9t - 4 = 0 \Leftrightarrow t = \frac{4}{9}\)
\( \Rightarrow B'\left( {\frac{4}{9};\frac{8}{9};\frac{{10}}{9}} \right)\)
Tương tự, C'(0; 1; 1)
c)
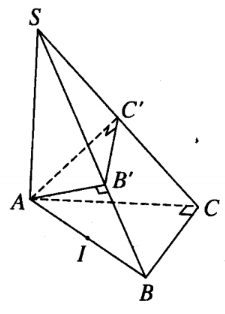
\(\overrightarrow {C'B'} = \left( {\frac{4}{9}; - \frac{1}{9};\frac{1}{9}} \right)\), \(\overrightarrow {AC'} = \left( {0;1;1} \right)\)
\( \Rightarrow \overrightarrow {C'B'} .\overrightarrow {AC'} = 0\) \( \Rightarrow C'B' \bot AC'\)
\( \Rightarrow {S_{AB'C'}} = \frac{1}{2}AC'.C'B'\) \( = \frac{1}{2}.\sqrt 2 .\sqrt {\frac{{16 + 1 + 1}}{{81}}} = \frac{1}{3}\)
Mà \(SB' = \sqrt {S{A^2} - AB{'^2}} \) \( = \sqrt {4 - \frac{{20}}{9}} = \frac{4}{3}\)
Vậy \({V_{S.AB'C'}} = \frac{4}{{27}}\).
d) Đường thẳng qua B và vuông góc với (P) có phương trình: \(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\\z = - 2t\end{array} \right.\)
Để tìm giao điểm Bo của đường thẳng này với (P) ta giải hệ
\(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\\z = - 2t\\x + 2y - 2z = 0\end{array} \right.\)\( \Rightarrow 1 + t + 2\left( {2 + 2t} \right) - 2\left( { - 2t} \right) = 0\) \( \Leftrightarrow 9t + 5 = 0 \Leftrightarrow t = - \frac{5}{9}\)
\( \Rightarrow {B_0}\left( {\frac{4}{9};\frac{8}{9};\frac{{10}}{9}} \right)\)
Từ đó suy ra điểm đối xứng với B qua (P) là \({B_1}\left( { - \frac{1}{9}; - \frac{2}{9};\frac{{20}}{9}} \right)\)
e) Dễ thấy \(\overrightarrow {BC} \bot \overrightarrow {AC} ,\overrightarrow {BC'} \bot \overrightarrow {AC'} ,\overrightarrow {BB'} \bot \overrightarrow {AB'} \) nên A, B, C, B', C' cùng thuộc mặt cầu tâm I(1/2; 1; 0) là trung điểm của AB, bán kính IA = (√5) /2
Phương trình mặt cầu đó là \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = \frac{5}{4}\)
Vì điểm C' thuộc mặt cầu, nên mặt phẳng tiếp xúc với mặt cầu tại C' phải vuông góc với \(\overrightarrow {IC'} = \left( { - \frac{1}{2};0;1} \right)\)
Phương trình của mặt phẳng đó là: x - 2(z - 1) = 0 hay x - 2z + 2 = 0.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9 trang 170 SBT hình học 12
- Bài 8 trang 169 SBT hình học 12
- Bài 7 trang 169 SBT hình học 12
- Bài 6 trang 169 SBT hình học 12
- Bài 5 trang 169 SBT hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
