-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 9 trang 170 SBT hình học 12
Giải bài 9 trang 170 sách bài tập hình học 12. Trong không gian Oxyz cho hình lập phương ABCD.A’B’C’D’ với A(0;0;0), B(1;0;0), D(0;1;0), A’(0;0;1)...
Đề bài
Trong không gian Oxyz cho hình lập phương ABCD.A’B’C’D’ với A(0;0;0), B(1;0;0), D(0;1;0), A’(0;0;1)
a) Hãy tìm tọa độ các đỉnh còn lại.
b) Chứng minh A'C ⊥ (BC'D)
c) Tìm tọa độ của chân đường vuông góc chung của B'D' và BC'.
Quảng cáo
Lời giải chi tiết
a) Dễ thấy C(1; 1; 0), B'(1; 0; 1), D'(0; 1; 1), C'(1; 1; 1), D'(0; 1; 1).
b) Ta có: \(\overrightarrow {A'C} = \left( {1;1; - 1} \right)\)
\(\overrightarrow {BC'} = \left( {0;1;1} \right)\), \(\overrightarrow {BD} = \overrightarrow {B'D'} = \left( { - 1;1;0} \right)\)
Do đó \(\overrightarrow {A'C} .\overrightarrow {BC'} = 0\) và \(\overrightarrow {A'C} .\overrightarrow {BD} = 0\)
Từ đó suy ra \(A'C \bot BC',A'C \bot BD\) nên A'C ⊥ (BC'D).
c)
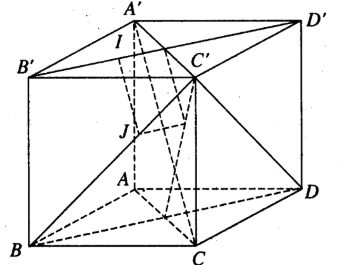
Gọi IJ là đường vuông góc chung của B'D' và BC'
\(\overrightarrow {{n_1}} \) là vectơ pháp tuyến của mặt phẳng (P) qua B'D' và song song với A’C
\(\overrightarrow {{n_2}} \) là vectơ pháp tuyến của mặt phẳng (Q) qua BC' và song song với A'C.
Khi đó \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {A'C} ,\overrightarrow {B'D'} } \right] = \left( {1;1;2} \right)\)
\(\overrightarrow {{n_2}} = \left[ {\overrightarrow {A'C} ,\overrightarrow {BC'} } \right] = \left( {2; - 1;1} \right)\)
Phương trình của (P) là: (x - 1) + y + 2(z - 1) = 0 hay x + y + 2z - 3 = 0.
Phương trình của (Q) là: 2(x - 1) - y + z = 0 hay 2x - y + z - 2 = 0.
Phương trình của (B'D') là: \(\left\{ \begin{array}{l}x = 1 - t\\y = t\\z = 1\end{array} \right.\) .
Phương trình của (BC') là: \(\left\{ \begin{array}{l}x = 1\\y = t\\z = t\end{array} \right.\)
I là giao điểm của đường thẳng B'D' và (Q), để tìm tọa độ của I ta thế phương trình đường thẳng B'D' vào phương trình của (Q)
Ta có: 2(1 - t) - t + 1 - 2 = 0, hay t = 1/3.
Từ đó suy ra I(2/3; 1/3; 1)
Tương tự, ta tìm được J(1; 2/3; 1/3).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 10 trang 170 SBT hình học 12
- Bài 8 trang 169 SBT hình học 12
- Bài 7 trang 169 SBT hình học 12
- Bài 6 trang 169 SBT hình học 12
- Bài 5 trang 169 SBT hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
