 Toán lớp 5, giải toán lớp 5, giải bài tập sgk toán 5 (sách mới)
Toán lớp 5, giải toán lớp 5, giải bài tập sgk toán 5 (sách mới)
 Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 5
Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 5 Đề kiểm tra học kì 1 Toán 5 - Đề số 9
Tải vềĐáp án và lời giải chi tiết Đề số 4 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 5
Đề bài
I. PHẦN TRẮC NGHIỆM (3 điểm)
Khoanh tròn vào chữ cái (A,B,C,D) trước câu trả lời đúng nhất
Câu 1. Số “ Tám mươi chín phẩy bảy mươi bảy” viết là:
A. 809,77 B. 89,77
C. 89,707 D. 98,77
Câu 2. Số lớn nhất trong các số 5,25; 5,52; 5,7; 5,58 là:
A. 5,52 B. 5,25
C. 5,7 D. 5,58
Câu 3. Số 0,55 viết dưới dạng tỉ số phần trăm là:
A. 0,55% B. 5,5%
C. 55% D. 550%
Câu 4. Giá trị của biểu thức 8,6 × (5,7 – 4,7 ) + 5,6 : 4 là:
A. 10 B. 12
C. 7,5 D. 3,55
Câu 5. 6dm2 15cm2 = ... dm2 . Số thích hợp điền vào chỗ chấm là:
A. 615 B. 61,5
C. 6,0015 D. 6,15
Câu 6. Một hình tam giác có độ dài đáy là 4,5cm, chiều cao 2,4cm. Tính điện tích hình tam giác đó.
A. 10,8cm2 B. 5,4cm2
C. 21,6cm2 D. 4,8cm2
II. PHẦN TỰ LUẬN
Bài 1. (2 điểm) Đặt tính rồi tính:
12,47 + 39,68
657,21 – 198,34
109,8 × 5,4
91,08 : 3,6
Bài 2. (2 điểm) Tìm \(x\):
a) 9,8 : \(x\) = 2,8 + 7
b) \(x\) + 25,6 = 86,5 : 2,5
Bài 3. (2 điểm) Một trại chăn nuôi có số gà và vịt là 1575 con, trong đó 40% là vịt, còn lại là gà. Hỏi trại chăn nuôi đó có bao nhiêu con gà, bao nhiêu con vịt ?
Bài 4. (1 điểm) Tính bằng cách thuận tiện nhất:
a) 16,9 + 8,4 + 3,1 + 1,6
b) 34,5 × 6,7 + 34,5 × 3,3
Lời giải
I. PHẦN TRẮC NGHIỆM
Câu 1.
Phương pháp:
Muốn viết một số thập phân, ta viết lần lượt từ hàng cao đến hàng thấp: trước hết viết phần nguyên, viết dấu "phấy", sau đó viết phần thập phân.
Cách giải:
Số “ Tám mươi chín phẩy bảy mươi bảy” viết là 89,77.
Chọn B.
Câu 2.
Phương pháp:
So sánh các số thập phân đã cho, từ đó tìm được số thập phân bé nhất trong các số đó.
* Cách so sán hai số thập phân:
- So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
- Nếu phần nguyên của hai số đó bằng nhau,thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
- Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.
Cách giải:
So sánh các số đã cho ta có:
5,25 < 5,52 < 5,58 < 5,7.
Vậy số lớn nhất trong các số đã cho là 5,7.
Chọn C.
Câu 3.
Phương pháp:
Muốn viết số 0,55 dưới dạng tỉ số phần trăm ta nhân 0,55 với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.
Cách giải:
Ta có: 0,55 = 55%.
Chọn C.
Câu 4.
Phương pháp:
- Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.
- Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau.
Cách giải:
8,6 × (5,7 – 4,7 ) + 5,6 : 4
= 8,6 × 1 + 1,4
= 8,6 + 1,4
= 10
Chọn A.
Câu 5.
Phương pháp:
- Xem lại cách viết các số đo diện tích dưới dạng số thập phân.
- Áp dụng cách chuyển đổi: 1dm2 = 100cm2 hay 1cm2 = \(\dfrac{1}{100}\)dm2 = 0,01dm2.
Cách giải:
Ta có: 6dm2 15cm2 = 6\(\dfrac{15}{100}\)dm2 = 6,15dm2.
Vậy số thập phân thích hợp để viết vào chỗ chấm của 6dm2 15cm2 = ... dm2 là 6,15.
Chọn D.
Câu 6.
Phương pháp:
Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
Cách giải:
Diện tích hình tam giác đó là:
4,5 × 2,4 : 2 = 5,4 (cm2)
Đáp số: 5,4cm2.
Chọn B.
II. PHẦN TỰ LUẬN
Bài 1.
Phương pháp:
Đặt tính rồi tính theo các quy tắc đã học về phép cộng, trừ, nhân, chia số thập phân.
Cách giải:
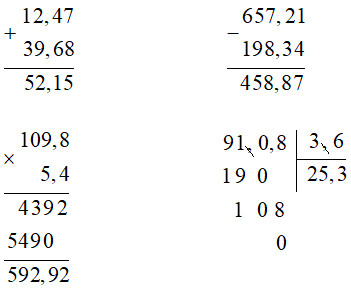
Bài 2.
Phương pháp:
- Tính giá trị vế phải trước.
- Áp dụng các quy tắc:
+ Muốn tìm số chia ta lấy số bị chia chia cho thương.
+ Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
Cách giải:
a) 9,8 : \(x\) = 2,8 + 7
9,8 : \(x\) = 9,8
\(x\) = 9,8 : 9,8
\(x\) = 1
b) \(x\) + 25,6 = 86,5 : 2,5
\(x\) + 25,6 = 34,6
\(x\) = 34,6 – 25,6
\(x\) = 9
Bài 3.
Phương pháp:
- Tìm số con gà ta lấy tổng số con gà và vịt (1575 con) chia cho 100 rồi nhân với 40 hoặc lấy tổng số con gà và vịt (1575 con) nhân với 40 rồi chia cho 100.
- Tìm số con vịt ta lấy tổng số con gà và vịt trừ đi số con gà.
Cách giải:
Trại chăn nuôi đó có số con gà là:
1575 : 100 × 40 = 630 (con)
Trại chăn nuôi đó có số con vịt là:
1575 – 630 = 945 (con)
Đáp số: Gà: 630 con ;
Vịt: 945 con.
Bài 4.
Phương pháp:
a) Áp dụng tính chất giao hoán và kết hợp để ghép 16,9 và 3,1 thành một nhóm, ghép 8,4 và 1,6 thành một nhóm.
b) Áp dụng công thức: a × b + a × c = a × (b + c).
Cách giải:
a) 16,9 + 8,4 + 3,1 + 1,6
= (16,9 + 3,1) + (8,4 + 1,6)
= 20 + 10
= 30
b) 34,5 × 6,7 + 34,5 × 3,3
= 34,5 × (6,7 + 3,3)
= 34,5 × 10
= 345
Loigiaihay.com











