-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Trả lời câu hỏi 1 trang 57 SGK Giải tích 12
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng...
Đề bài
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng:
\(y = {x^2};\,y = {x^{{1 \over 2}}};\,y = {x^{ - 1}}\)
Video hướng dẫn giải
Lời giải chi tiết
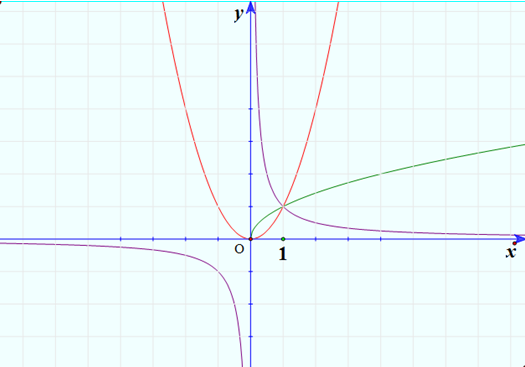
Đồ thị của hàm số \(y = {x^2}\): đường màu đỏ.
Đồ thị của hàm số \(y = {x^{{1 \over 2}}}\): đường màu xanh.
Đồ thị của hàm số \(y = {x^{ - 1}}\): đường màu tím.
Ta có:
Tập xác định của hàm số \(y = {x^2}\) là \(\mathbb R.\)
Tập xác định của hàm số \(y = {x^{{1 \over 2}}}\) là \(\left( {0, + \infty } \right)\).
Tập xác định của hàm số \(y = {x^{ - 1}}\) là \(\mathbb R \backslash \left\{ 0 \right\}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Trả lời câu hỏi 2 trang 57 SGK Giải tích 12
- Trả lời câu hỏi 3 trang 58 SGK Giải tích 12
- Giải bài 1 trang 60 SGK Giải tích 12
- Giải bài 2 trang 61 SGK Giải tích 12
- Giải bài 3 trang 61 SGK Giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
