Bài 73 trang 17 SBT Hình học 11 Nâng cao

Giải bài 73 trang 17 sách bài tập Hình học 11 Nâng cao. Cho đường triòn (O) và một điểm P nằm trong đường tròn đó. Một đường thẳng thay đổi đi qua P, cắt (O) tại hai điểm A và B...

Đề bài

Cho đường triòn (O) và một điểm P nằm trong đường tròn đó. Một đường thẳng thay đổi đi qua P, cắt (O) tại hai điểm A và B. Tìm quỹ tích điểm M sao cho \(\overrightarrow {PM} = \overrightarrow {PA} + \overrightarrow {PB} \).

Lời giải chi tiết

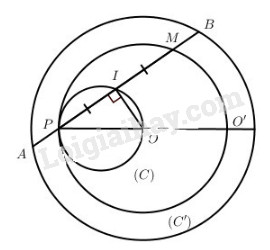
Gọi I là trung điểm của AB thì \(\overrightarrow {PI} = {{\overrightarrow {PA} + \overrightarrow {PB} } \over 2}\) , bởi vậy \(\overrightarrow {PM} = \overrightarrow {PA} + \overrightarrow {PB} = 2\overrightarrow {PI} \).

Gọi V là phép vị tự tâm P tỉ số k = 2 thì V biến điểm I thành điểm M.

Vì I là trung điểm của AB nên OI ⊥ AB. Suy ra quỹ tích của điểm I là đường tròn (C) đườn kính PO.

Vậy quỹ tích của điểm M là đường tròn (C’) ảnh của (C) qua phép vị tự V. Nếu ta lấy O’ sao cho \(\overrightarrow {PO'} = 2\overrightarrow {PO} \) thì (C’) là đường tròn đường kính PO’.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 74 trang 17 SBT Hình học 11 Nâng cao
Giải bài 74 trang 17 sách bài tập Hình học 11 Nâng cao. Cho điểm A cố định nằm trên đường tròn (O) và điểm C thay đổi trên đường tròn đó. Dựng hình vuông ABCD. Tìm quỹ tích điểm B và điểm D.
Bài 72 trang 17 SBT Hình học 11 Nâng cao
Giải bài 72 trang 17 sách bài tập Hình học 11 Nâng cao. Cho đường tròn (O) với dây cung PQ. Dựng hình vuông ABCD có hai đỉnh A, B nằm trên đường thẳng PQ và hai đỉnh C, D nằm trên đường tròn.
Bài 71 trang 16 SBT Hình học 11 Nâng cao
Giải bài 71 trang 16 sách bài tập Hình học 11 Nâng cao. Cho phép vị tự V tâm O, tỉ số k ≠ 1 và phép tịnh tiến T theo vectơ...
Bài 70 trang 16 SBT Hình học 11 Nâng cao
Giải bài 70 trang 16 sách bài tập Hình học 11 Nâng cao. Cho hai đường tròn có bán kính bằng nhau (O) và (O’)...
Bài 69 trang 16 SBT Hình học 11 Nâng cao
Giải bài 69 trang 16 sách bài tập Hình học 11 Nâng cao. Cho hai đường thẳng phân biệt a, a’ và phép dời hình F biến a thành a’...
Bài 68 trang 16 SBT Hình học 11 Nâng cao
Giải bài 68 trang 16 sách bài tập Hình học 11 Nâng cao. Cho hai đoạn thẳng bằng nhau AB và A’B; (AB = A’B;). Chứng minh rằng có một phép đối xứng trượt biến A thành A’, biến B thành B’.
Bài 67 trang 16 SBT Hình học 11 Nâng cao
Giải bài 67 trang 16 sách bài tập Hình học 11 Nâng cao. Cho Đ là phép đối xứng trục có trục đối xứng là đường thẳng d và T là phép tịnh tiến theo vectơ...
Bài 66 trang 16 SBT Hình học 11 Nâng cao
Giải bài 66 trang 16 sách bài tập Hình học 11 Nâng cao. Cho đường tròn (O) và phép dời hình F biến (O) thành chính nó nhưng F không phải là phép đồng nhất...
Bài 65 trang 15 SBT Hình học 11 Nâng cao
Giải bài 65 trang 15 sách bài tập Hình học 11 Nâng cao. Cho phép dời hình F không phải là phép đồng nhất. ...
Bài 64 trang 15 SBT Hình học 11 Nâng cao
Giải bài 64 trang 15 sách bài tập Hình học 11 Nâng cao. Cho hai điểm A và A’ đối xứng với nhau qua điểm I, F là phép dời hình biến I thành I, biến A thành A’. Chứng minh rằng F là phép đối xứng tâm hoặc đối xứng trục.