-
ĐẠI SỐ VÀ GIẢI TÍCH - SBT TOÁN 11 NÂNG CAO
-
CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
-
CHƯƠNG 2: TỔ HỢP VÀ XÁC SUẤT
-
CHƯƠNG 3: DÃY SỐ, CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN
-
CHƯƠNG 4: GIỚI HẠN
- Bài 1: Dãy số có giới hạn 0
- Bài 2: Dãy có giới hạn hữu hạn
- Bài 3: Dãy có giới hạn vô cực
- Bài 4: Định nghĩa và một số định lí về giới hạn của hàm số
- Bài 5. Giới hạn một bên
- Bài 6: Một vài quy tắc tìm giới hạn vô cực
- Bài 7: Các dạng vô định
- Bài 8: Hàm số liên tục
- Ôn tập chương IV - Giới hạn - SBT Toán 11 Nâng cao
-
CHƯƠNG 5: ĐẠO HÀM
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH
-
-
HÌNH HỌC-SBT TOÁN 11 NÂNG CAO
-
CHƯƠNG 1: PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG
- Bài 1, 2: Mở đầu về phép biến hình. Phép tịnh tiến và phép dời hình
- Bài 3: Phép đối xứng trục
- Bài 4: Phép quay và phép đối xứng tâm
- Bài 5: Hai hình bằng nhau
- Bài 6, 7: Phép vị tự. Phép đồng dạng
- Ôn tập chương 1: Phép dời hình và phép đồng dạng
- Bài tập trắc nghiệm chương 1 - Phép dời hình và phép đồng dạng
-
CHƯƠNG 2: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
-
CHƯƠNG 3. VECTƠ KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
- Bài 1. Vectơ trong không gian. Sự đồng phẳng của các vectơ
- Bài 2, 3, 4: Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc
- Bài 5: Khoảng cách
- Ôn tập chương III. Vectơ trong không gian. Quan hệ vuông góc
- Bài tập trắc nghiệm chương III. Vectơ trong không gian. Quan hệ vuông góc.
-
ÔN TẬP CUỐI NĂM - HÌNH HỌC
-
Bài 68 trang 16 SBT Hình học 11 Nâng cao
Giải bài 68 trang 16 sách bài tập Hình học 11 Nâng cao. Cho hai đoạn thẳng bằng nhau AB và A’B; (AB = A’B;). Chứng minh rằng có một phép đối xứng trượt biến A thành A’, biến B thành B’.
Đề bài
Cho hai đoạn thẳng bằng nhau AB và A’B; (AB = A’B;). Chứng minh rằng có một phép đối xứng trượt biến A thành A’, biến B thành B’.
Quảng cáo
Lời giải chi tiết
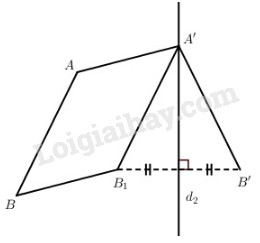
Gọi T là phép tịnh tiến theo vectơ \(\overrightarrow v = \overrightarrow {AA'} \) .
Khi đó T biến A thành A’ và biến B thành B1.
Gọi d2 là đường trung trực của đoạn thẳng B1B’ nếu B1 khác B’, còn nếu B1 trùng B’ thì lấy d2 là đường thẳng A’B’.
Hiển nhiên khi đó d2 đi qua A’ và phép đối xứng Đ2 qua đường thẳng d2 biến A’ thành A’ và biến B1 thành B’.
Vậy hợp thành F của T và Đ2 sẽ biến A thành A’ và biến B thành B’.
Suy ra F là phép đối xứng trượt.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 69 trang 16 SBT Hình học 11 Nâng cao
- Bài 70 trang 16 SBT Hình học 11 Nâng cao
- Bài 71 trang 16 SBT Hình học 11 Nâng cao
- Bài 72 trang 17 SBT Hình học 11 Nâng cao
- Bài 73 trang 17 SBT Hình học 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
