-
ĐẠI SỐ VÀ GIẢI TÍCH - SBT TOÁN 11 NÂNG CAO
-
CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
-
CHƯƠNG 2: TỔ HỢP VÀ XÁC SUẤT
-
CHƯƠNG 3: DÃY SỐ, CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN
-
CHƯƠNG 4: GIỚI HẠN
- Bài 1: Dãy số có giới hạn 0
- Bài 2: Dãy có giới hạn hữu hạn
- Bài 3: Dãy có giới hạn vô cực
- Bài 4: Định nghĩa và một số định lí về giới hạn của hàm số
- Bài 5. Giới hạn một bên
- Bài 6: Một vài quy tắc tìm giới hạn vô cực
- Bài 7: Các dạng vô định
- Bài 8: Hàm số liên tục
- Ôn tập chương IV - Giới hạn - SBT Toán 11 Nâng cao
-
CHƯƠNG 5: ĐẠO HÀM
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH
-
-
HÌNH HỌC-SBT TOÁN 11 NÂNG CAO
-
CHƯƠNG 1: PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG
- Bài 1, 2: Mở đầu về phép biến hình. Phép tịnh tiến và phép dời hình
- Bài 3: Phép đối xứng trục
- Bài 4: Phép quay và phép đối xứng tâm
- Bài 5: Hai hình bằng nhau
- Bài 6, 7: Phép vị tự. Phép đồng dạng
- Ôn tập chương 1: Phép dời hình và phép đồng dạng
- Bài tập trắc nghiệm chương 1 - Phép dời hình và phép đồng dạng
-
CHƯƠNG 2: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
-
CHƯƠNG 3. VECTƠ KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
- Bài 1. Vectơ trong không gian. Sự đồng phẳng của các vectơ
- Bài 2, 3, 4: Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc
- Bài 5: Khoảng cách
- Ôn tập chương III. Vectơ trong không gian. Quan hệ vuông góc
- Bài tập trắc nghiệm chương III. Vectơ trong không gian. Quan hệ vuông góc.
-
ÔN TẬP CUỐI NĂM - HÌNH HỌC
-
Bài 58 trang 14 SBT Hình Học 11 Nâng cao
Giải bài 58 trang 14 sách bài tập Hình Học 11 Nâng cao. Chứng minh rằng B’C’ là đường kính của (O3).
Đề bài
Cho ba đường tròn (O1), (O2), (O3) đôi một tiếp xúc ngoài với nhau, A là tiếp điểm của (O1) và (O2); B là tiếp điểm (O2) và (O3); C là tiếp điểm của (O3) và (O1). Đường thẳng AB cắt (O3) tại điểm thứ hai C’. Chứng minh rằng B’C’ là đường kính của (O3).
Lời giải chi tiết
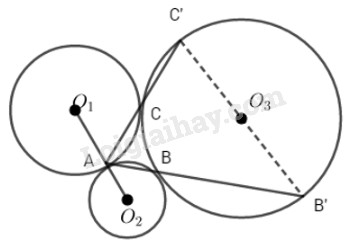
Vì B là tâm vị tự trong của (O2) và (O3) nên O2A // O3B’.
Vì C là tâm vị tự trong của (O1) và (O3) nên O1A // O3C’.
Vì ba điểm O1, A, O2 thẳng hàng nên C’, O3, B’ thẳng hàng.
Như vậy B’C’ là đường kính của đường tròn (O3).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 59 trang 15 SBT Hình Học 11 Nâng cao
- Bài 60 trang 15 SBT Hình Học 11 Nâng cao
- Bài 61 trang 15 SBT Hình Học 11 Nâng cao
- Bài 62 trang 15 SBT Hình Học 11 Nâng cao
- Bài 63 trang 15 SBT Hình Học 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
