Câu 4 trang 114 Sách bài tập Hình học 11 Nâng cao

Giải bài tập Câu 4 trang 114 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình chóp S.ABCD có đáy là hình bình hành. Một mặt phẳng (P) bất kì không đi qua S, cắt các cạnh bên SA, SB, SC, SD lần lượt tại các điểm \({A_1},{B_1},{C_1},{D_1}\) . Dùng phương pháp vectơ, chứng minh rằng

\({{SA} \over {S{A_1}}} + {{SC} \over {S{C_1}}} = {{SB} \over {S{B_1}}} + {{S{\rm{D}}} \over {S{{\rm{D}}_1}}}\)

Lời giải chi tiết

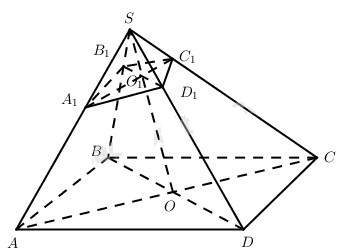
Vì ABCD là hình bình hành nên

\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {S{\rm{D}}} \)

hay \(\overrightarrow {S{\rm{D}}} = \overrightarrow {SA} + \overrightarrow {SC} - \overrightarrow {SB} \)

Đặt

\(\eqalign{ & \overrightarrow {SA} = a\overrightarrow {S{A_1}} ,\overrightarrow {SB} = b\overrightarrow {S{B_1}} , \cr & \overrightarrow {SC} = c\overrightarrow {S{C_1}} ,\overrightarrow {S{\rm{D}}} = d\overrightarrow {S{{\rm{D}}_1}} \cr} \)

(với a, b, c, d là các số lớn hơn 1)

Khi đó:

\(\eqalign{ & {{SA} \over {S{A_1}}} + {{SC} \over {S{C_1}}} = a + c \cr & {{SB} \over {S{B_1}}} + {{S{\rm{D}}} \over {S{{\rm{D}}_1}}} = b + d \cr} \)

và

\(\eqalign{ & \overrightarrow {S{{\rm{D}}_1}} = {1 \over d}.\overrightarrow {S{\rm{D}}} = {1 \over d}\left( {\overrightarrow {SA} + \overrightarrow {SC} - \overrightarrow {SB} } \right) \cr & = {1 \over d}\left( {a\overrightarrow {S{A_1}} + c\overrightarrow {S{C_1}} - b\overrightarrow {S{B_1}} } \right) \cr & = {a \over d}.\overrightarrow {S{A_1}} + {c \over d}.\overrightarrow {S{C_1}} - {b \over d}.\overrightarrow {S{B_1}} \cr} \)

Mặt khác các điểm \({A_1},{B_1},{C_1},{D_1}\) thuộc mặt phẳng, nên từ đẳng thức đó suy ra

\({a \over d} + {c \over d} - {b \over d} = 1\)

tức là a + c = b + d

Như vậy \({{SA} \over {S{A_1}}} + {{SC} \over {S{C_1}}} = {{SB} \over {S{B_1}}} + {{S{\rm{D}}} \over {S{{\rm{D}}_1}}}\).

Loigiaihay.com