Bài 27 trang 9 SBT Hình Học 11 nâng cao

Giải bài 27 trang 9 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng m chỉ cắt (P) tại điểm chung duy nhất M. (Đường thẳng m như thế được gọi là tiếp tuyến của (P) tại điểm M).

Đề bài

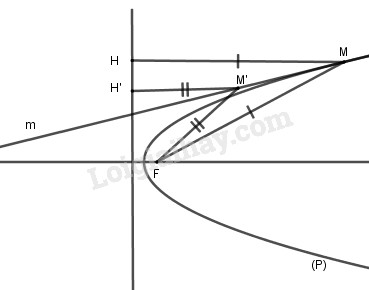
Cho parabol (P) có tiêu điểm F và đường chuẩn d. Với điểm M trên (P) ta kẻ \(MH \bot d\,(H \in d)\) và gọi m là phân giác của góc FMH. Chứng minh rằng m chỉ cắt (P) tại điểm chung duy nhất M. (Đường thẳng m như thế được gọi là tiếp tuyến của (P) tại điểm M).

Lời giải chi tiết

Vì M nằm trên parabol (P) nên MF = MH.

Do đó m chính là đường trung trực của đoạn thẳng FH.

Lấy điểm M’ tùy ý nằm trên m, kẻ \(M'H' \bot d\,\left( {H' \in \,d} \right)\) thì ta có: \(M'F = M'H \ge M'H'.\)

Nếu M’ không trùng với M thì M’F > M’H’ nên M’ không nằm trên (P).

Vậy M chỉ cắt (P) tại điểm duy nhất M.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 28 trang 9 SBT Hình Học 11 nâng cao
Giải bài 28 trang 9 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng các đường thẳng AA’, BB’, CC’ đồng quy.
Bài 29 trang 9 SBT Hình Học 11 nâng cao
Giải bài 29 trang 9 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng các đường thẳng đi qua A’ vuông góc với BC, qua B’ vuông góc với AC, qua C’ vuông góc với AB đồng quy.
Bài 26 trang 9 SBT Hình Học 11 nâng cao
Giải bài 26 trang 9 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng m chỉ cắt (H) tại điểm M duy nhất.( Đường thẳng m như thế được gọi là tiếp tuyến của (H) tại điểm M).
Bài 25 trang 9 SBT Hình Học 11 nâng cao
Giải bài 25 trang 9 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng m chỉ cắt (E) tại điểm M duy nhất (đường thẳng m như thế được gọi là tiếp tuyến của (E) tại điểm M).
Bài 24 trang 9 SBT Hình Học 11 nâng cao
Giải bài 24 trang 9 sách bài tập Hình Học 11 nâng cao. Gọi m là đường phân giác ngoài tại A của tam giác ABC. Chứng minh rằng với mọi điểm M trên m, chu vi của tam giác MBC không nhỏ hơn chu vi tam giác ABC.
Bài 23 trang 8 SBT Hình Học 11 nâng cao
Giải bài 23 trang 8 sách bài tập Hình Học 11 nâng cao. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d và đường tròn (C) lần lượt có phương trình.
Bài 22 trang 8 SBT Hình Học 11 nâng cao
Giải bài 22 trang 8 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng chỉ cần tối đa ba phép đối xứng trục để hợp thành của chúng biến tam giác ABC thành tam giác A’B’C’.
Bài 21 trang 8 SBT Hình Học 11 nâng cao
Giải bài 21 trang 8 sách bài tập Hình Học 11 nâng cao. Cho hai đoạn thẳng bằng nhau AB = A’B’. Chứng minh rằng có thể tìm được một phép đối xứng trục hoặc hợp thành của hai phép đối xứng trục để biến A thành A’, biến B thành B’.
Bài 20 trang 8 SBT Hình Học 11 nâng cao
Giải bài 20 trang 8 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng: a) Hợp thành của hai phép đối xứng trục có các trục đối xứng song song là một phép tịnh tiến.
Bài 19 trang 8 SBT Hình Học 11 nâng cao
Giải bài 19 trang 8 sách bài tập Hình Học 11 nâng cao. Cho hai điểm A, B phân biệt. Có những phép dời hình nào biến A thành A và biến B thành B.
Bài 18 trang 8 SBT Hình Học 11 nâng cao
Giải bài 18 trang 8 sách bài tập Hình Học 11 nâng cao. Cho hai điểm phân biệt A, B và phép dời hình F khác với phép đồng nhất sao cho F(A) = A, F(B) = B.