-
ĐẠI SỐ VÀ GIẢI TÍCH - SBT TOÁN 11 NÂNG CAO
-
CHƯƠNG 1: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
-
CHƯƠNG 2: TỔ HỢP VÀ XÁC SUẤT
-
CHƯƠNG 3: DÃY SỐ, CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN
-
CHƯƠNG 4: GIỚI HẠN
- Bài 1: Dãy số có giới hạn 0
- Bài 2: Dãy có giới hạn hữu hạn
- Bài 3: Dãy có giới hạn vô cực
- Bài 4: Định nghĩa và một số định lí về giới hạn của hàm số
- Bài 5. Giới hạn một bên
- Bài 6: Một vài quy tắc tìm giới hạn vô cực
- Bài 7: Các dạng vô định
- Bài 8: Hàm số liên tục
- Ôn tập chương IV - Giới hạn - SBT Toán 11 Nâng cao
-
CHƯƠNG 5: ĐẠO HÀM
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH
-
-
HÌNH HỌC-SBT TOÁN 11 NÂNG CAO
-
CHƯƠNG 1: PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG
- Bài 1, 2: Mở đầu về phép biến hình. Phép tịnh tiến và phép dời hình
- Bài 3: Phép đối xứng trục
- Bài 4: Phép quay và phép đối xứng tâm
- Bài 5: Hai hình bằng nhau
- Bài 6, 7: Phép vị tự. Phép đồng dạng
- Ôn tập chương 1: Phép dời hình và phép đồng dạng
- Bài tập trắc nghiệm chương 1 - Phép dời hình và phép đồng dạng
-
CHƯƠNG 2: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
-
CHƯƠNG 3. VECTƠ KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
- Bài 1. Vectơ trong không gian. Sự đồng phẳng của các vectơ
- Bài 2, 3, 4: Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc
- Bài 5: Khoảng cách
- Ôn tập chương III. Vectơ trong không gian. Quan hệ vuông góc
- Bài tập trắc nghiệm chương III. Vectơ trong không gian. Quan hệ vuông góc.
-
ÔN TẬP CUỐI NĂM - HÌNH HỌC
-
Bài 25 trang 9 SBT Hình Học 11 nâng cao
Giải bài 25 trang 9 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng m chỉ cắt (E) tại điểm M duy nhất (đường thẳng m như thế được gọi là tiếp tuyến của (E) tại điểm M).
Đề bài
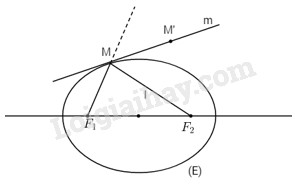
Cho elip (E) với hai tiêu điểm \({F_1}\) và \({F_2}\) . Gọi M là một điểm nằm trên (E) nhưng không nằm trên đường thẳng \({F_1}{F_2}\) và m là phân giác ngoài tại đỉnh M của tam giác \(M{F_1}{F_2}\).
Chứng minh rằng m chỉ cắt (E) tại điểm M duy nhất (đường thẳng m như thế được gọi là tiếp tuyến của (E) tại điểm M).
Lời giải chi tiết
Giả sử elip (E) có trục lớn là 2a, tức là điểm M nằm trên (E) khi và chỉ khi:
\(M{F_1} + M{F_2} = 2a\)
Theo chứng minh bài tập 24, nếu M’ nằm trên phân giác m thì:
\(M'{F_1} + M'{F_2} \ge M{F_1} + M{F_2} = 2a.\)
Dấu bằng xảy ra khi và chỉ khi M’ trùng M. Vậy nếu M’ khác M thì M’ không nằm trên (E).
Từ đó, suy ra m cắt (E) tại điểm duy nhất M.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 26 trang 9 SBT Hình Học 11 nâng cao
- Bài 27 trang 9 SBT Hình Học 11 nâng cao
- Bài 28 trang 9 SBT Hình Học 11 nâng cao
- Bài 29 trang 9 SBT Hình Học 11 nâng cao
- Bài 24 trang 9 SBT Hình Học 11 nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
