Giải SBT toán hình học và đại số 10 nâng cao Bài 3. Hệ thức lượng trong tam giác.

Bài 68 trang 49 SBT Hình học 10 Nâng cao


Giải bài tập Bài 68 trang 49 SBT Hình học 10 Nâng cao

Đề bài

Từ một vị trí quan sát \(A\) cố định trên bờ biển, người ta muốn tính khoảng cách đến một vị trí \(B\) trên mặt biển bằng giác kế (máy đo góc). Em có thế làm việc đó bằng cách nào ?

Lời giải chi tiết

(h.61).

 

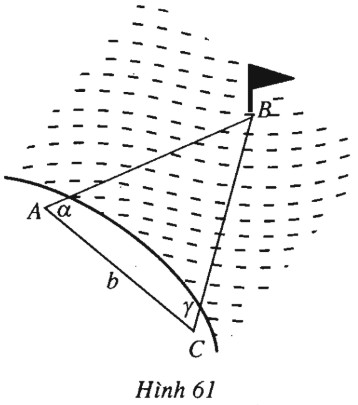
Chọn vị trí \(C\) thích hợp trên bờ cách điểm \(A\) một khoảng bằng \(b\).

Sau đó dùng giác kế đo các góc được \(\widehat A = \alpha  ,  \widehat C = \gamma \).

Áp dụng định lí sin:  \(\dfrac{{AB}}{{\sin C}} = \dfrac{{AC}}{{\sin B}}\), ta tính được:

\(AB = \dfrac{{Ac\sin C}}{{\sin B}}\)

\(= \dfrac{{b\sin \gamma }}{{\sin \left[ {{{180}^0} - \left( {\alpha  + \gamma } \right)} \right]}}\)

\(= \dfrac{{b\sin \gamma }}{{\sin \left( {\alpha  + \gamma } \right)}}\).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store